Ampere's Circuital Law and its Application to Infinitely Long Straight Wire
Important Questions on Ampere's Circuital Law and its Application to Infinitely Long Straight Wire
"Increasing the current sensitivity of a galvanometer may not necessarily increase its voltage sensitivity". Justify this statement.
Why is it necessary to introduce a cylindrical soft iron core inside the coil of a galvanometer?
Use this expression to define SI unit of current.
Derive a mathematical expression for the force acting on a current carrying straight conductor kept in a magnetic field. State the rule used to determine the direction of this force. Under what conditions this force (i) zero and (ii) maximum?
Using Ampere's circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
An observer to the left of a solenoid of turns each of cross-section area observes that a steady current in it flows in the clockwise direction. Depict the magnetic field lines due to the solenoid specifying its polarity and show that it acts as a bar magnet of magnetic moment .

State Ampere's circuital law. Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius , having turns per unit length and carrying a steady current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero.
Show how Biot-Savart law can be alternatively expressed in the form of Ampere's circuital law. Use this law to obtain the expression for the magnetic field inside a solenoid of length , cross-sectional area having closely wound turns and carrying a steady current .
Use Ampere's law to derive the formula for the magnetic field due to an infinitely long straight current carrying wire.
State Ampere's circuital law connecting the line integral of over a closed path to the net current crossing the area bounded by the path.
A long straight wire of a circular cross-section of radius carries a steady current . The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point in the region for .
A long straight wire of a circular cross-section of radius carries a steady current . The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point in the region for .
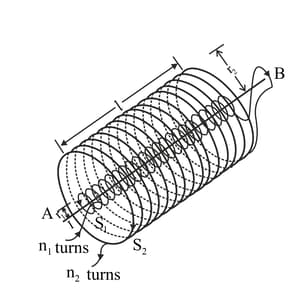
Two long coaxial insulated solenoids, and of equal lengths are wound one over the other, as shown in the figure. A steady current " flows through the inner solenoid to the other end , which is connected to the outer solenoid through which the same current " flows in the opposite direction so as to come out at end . If and are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point outside the combined system.
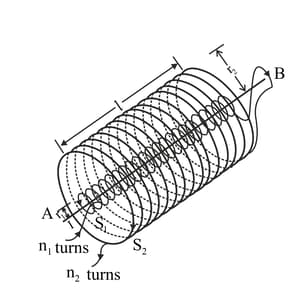
Two long coaxial insulated solenoids, and of equal lengths are wound one over the other, as shown in the figure. A steady current " flows through the inner solenoid to the other end , which is connected to the outer solenoid through which the same current " flows in the opposite direction so as to come out at end . If and are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point inside on the axis.
State Ampere's circuital law, expressing it in the integral form.
Show that in an ideal toroid, the magnetic field outside the toroid at any point in the open space is zero.
Use Ampere's circuital law to obtain the magnetic field inside a toroid.
A long solenoid with closely wound turns has turns, per unit of its length. A steady current flows through this solenoid. Use Ampere's circuital law to obtain an expression, for the magnetic field, at a point on its axis and close to its midpoint. Draw its field lines.
State Ampere's circuital law. Use this law to find magnetic field due to straight infinite current.
State Ampere's circuital law and prove this law for a circular path around a long current carrying conductor.

