Magnetic Field Due to a Current Carrying Circular Coil

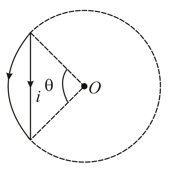
Net magnetic field at the centre of the circle $O$ due to a current carrying loop as shown in figure is $\left(\theta <{180}^{\circ }\right)$

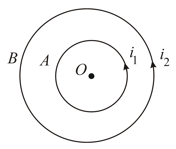
$A$ and $B$ are two concentric circular conductors of centre $O$ and carrying current $i_1$ and $i_2$ as shown in the diagram. If ratio of their radii $1:2$ and ratio of the flux densities at $O$ due to $A$ and $B$ is $1:3$ then the value of $\frac{i_1}{i_2}$ will be-

Value of earth's magnetic field at any point is $7\times {10}^{-5} \mathrm{wb} {\mathrm{m}}^{-2}$. This field is neutralised by field which is produced at the centre of a current carrying loop of radius $5 \mathrm{cm}$. The current in the loop (approx)

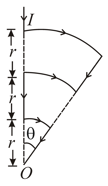
A conductor carrying a current, $I$ is shown in the figure. Calculate the magnetic field intensity at the point $O$ (common center of all three arcs). Use $I=2 \mathrm{A}, \theta =48 \mathrm{rad}$ and $r=2\mu \mathrm{m}$

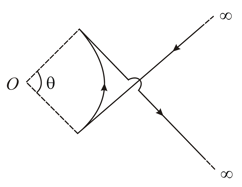
If magnetic field at point $O$ is zero then find out the value of $\theta$ (in radian).

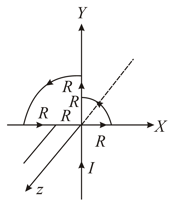
Find the magnetic induction at the origin in the figure shown.

Two coils each of $100$ turns are held such that one lies in the vertical plane with their centres coinciding. The radius of the vertical coil is $20 \mathrm{cm}$ and that of the horizontal coil is $30 \mathrm{cm}$. How would you neutralize the magnetic field of the earth at their common centre? What is the current to be passed through each coil? Horizontal component of earth's magnetic induction $=3.49\times {10}^{-5}\mathrm{T}$ and angle of dip $=30°$. 

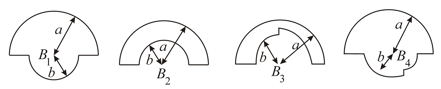
In the loops shown, all curved section are semicircles or quarter circles. All the loops carry the same current. The magnetic fields at the centres have magnitudes $B_1, B_2, B_3$ and $B_4$

If the intensity of magnetic field at a point on the axis of current coil is half of that at the centre of the coil, then the distance of that point from the centre of the coil will be

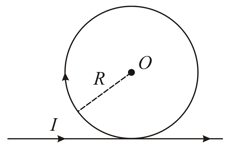
An infinitely long straight conductor is bent into the shape as shown in figure. It carries a current $I$ ampere and the radius of the circular loop is $r$ meter. Then the magnetic induction at the centre of the circular part is

Two concentric coils each of radius equal to $2\pi \mathrm{cm}$ are placed at right angles to each other, $3 \mathrm{A}$ and $4 \mathrm{A}$ are the currents flowing in each coil, respectively. The magnetic induction in $\mathrm{Wb} {\mathrm{m}}^{-2}$ at the centre of the coils will be $\left({\mu }_0=4\pi \times {10}^{-7}\mathrm{Wb} {\mathrm{A}}^{-1} {\mathrm{m}}^{-1}\right)$

Two concentric circular coils X and Y of radii $16 \mathrm{cm}$ and $10 \mathrm{cm}$, respectively, lie in the same vertical plane containing the north to south direction. Coil X has $20$ turns and carries a current of $16 \mathrm{A}$; coil Y has $25 \mathrm{turns}$ and carries a current of $18 \mathrm{A}$. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.