Simple and Compound Pendulum

A disc of radius $R$ is suspended from its circumference and made to oscillate. Its length equivalent to a simple pendulum will be

A disc of radius $R$ is suspended from its circumference and made to oscillate. Its time period will be:

A ring of radius $R$ is suspended from its circumference and is made to oscillate about a horizontal axis in a vertical plane. The length equivalent to a simple pendulum will be

For a compound pendulum, the maximum time period is

The distance between the points of suspension and centre of oscillation for a compound pendulum is $l$, and radius of gyration is $k$. Its time period is ?

The distance of point of a compound pendulum from its centre of gravity is $l$, the time period of oscillation relative to this point is $T$. If $g={\pi }^2$, the relation between $l$ and $T$ will be,

In the compound pendulum, the minimum period of oscillation will be,

The distance between the point of suspension and the centre of gravity of a compound pendulum is $l$ and the radius of gyration about the horizontal axis through the centre of gravity is $k$. Then, its time period will be,

The time period of oscillation of a simple pendulum having length $L$ and mass of the bob $m$ is given as $T$. If the length of the pendulum is increased to $4L$ and the mass of the bob is increased to $2m$, then which one of the following is the new time period of oscillation?

The time period of a simple pendulum is given by, $T=2\pi \sqrt{\frac{l}{g}}$. In an experiment, the length of the pendulum is increased by $1\%$ while the acceleration due to gravity is also increased by $2\%$. The time period will,

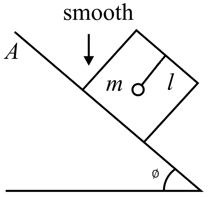
A box placed on a smooth inclined plane is free to move. Find the time period of oscillation of the simple pendulum attached to the ceiling of the box.

If the length of a simple pendulum is comparable to the radius of the earth, then find the time period for oscillation.

A simple pendulum attached to the ceiling of a stationary lift has a time period $T$ . The distance $y$ covered by the lift moving upwards varies with time $t$ as, $y=t^2$, where $y$ is in $\mathrm{metres}$ and $t$ in $\sec$. If $g=10 \mathrm{m} {\mathrm{s}}^{-2}$, then the time period of the pendulum will be,

A simple pendulum is suspended from the ceiling of a lift. When the lift is at rest, its time period is $T$. With what acceleration should the lift be accelerated upwards in order to reduce its period to $\frac{T}{2}$? ($g$ is the acceleration due to gravity)

A metre stick swinging about its one end oscillates with frequency $f_0$. If the bottom half of the stick was cut off, then its new oscillation frequency will be:

The bob of a simple pendulum executes simple harmonic motion in water with a period $t$, while the period of oscillation of the bob is $t_0$ in air. Neglecting frictional force of water and given that the density of the bob is $\left(\frac{4}{3}\right)\times 1000 \mathrm{kg}/{\mathrm{m}}^3$, which relationship between $t$ and $t_0$ is true? 

If the length of second pendulum is increased by $2\%$, how many seconds it will lose per day?

What is the effect on the time period of a simple pendulum if the mass of the bob is doubled?