Conservation of Angular Momentum

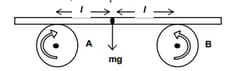
A uniform bar with mass $m=16\mathrm{kg}$ lies symmetrically across two rapidly rotating fixed rollers, $A$ and $B$ with distance '$\ell =8\mathrm{m}$' between the bars centre of mass and each roller. The rollers whose direction of rotation are shown in figure slip against the bar with coefficient of friction $\mu =0.2$. Suppose the bar is displaced horizontally by a small distance '$x$' and then released, the time period of oscillation in sec is.

A circular disc of mass $M$ and radius $R$ is rotating about its axis with angular speed ${\omega }_1.$ If another stationary disc having radius $\frac{R}{2}$ and same mass $M$ is droped co-axially on to the rotating disc. Gradually both discs attain constant angular speed ${\omega }_2$ the energy lost in the process is $p\%$ of the initial energy. Value of $p$ is

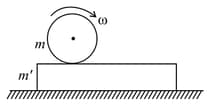
A uniform solid cylinder is given an angular speed $\omega$ and placed on a rough plate of negligible thickness. The horizontal surface below the plate is smooth. Then the angular speed of the cylinder when it starts pure rolling on the plate will be: [Assume sufficient length of plate]

A hoop of radius $r$ and mass $m$ rotating with angular velocity ${\omega }_0$ is placed on a rough horizontal surface. The initial velocity of centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?

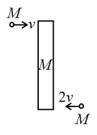
Two masses $\left(M\right)$ are moving perpendicular to the rod of mass $M$ with velocities $v\text{ and} 2v$ as shown in the figure. The length of the rod is $L$. Find the ratio of the final velocity of the rod and its angular velocity if the masses stop at their place after collision.

A hollow sphere is set into motion on a rough horizontal surface with a speed $v$ in the forward direction and a rotational speed $v/R$ in the anticlockwise direction as shown in the figure. Find the translational speed of the sphere $\left(\mathrm{a}\right)$ when it stops rotating and $\left(\mathrm{b}\right)$ when slipping finally ceases and pure rolling starts.

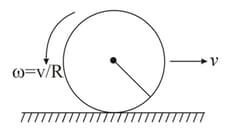
A solid sphere is rolling without slipping on a rough ground as shown in figure. It collides elastically with an identical another sphere at rest. There is no friction between the two spheres. Radius of each sphere is $R$ and mass is $m$. The linear velocity of first sphere after it again starts rolling without slipping is,

A merry-go-round, made of a ring-like platform of radius $R$ and mass$M$, is revolving with angular speed$\text{ω}$. A person of mass$M$ is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round of afterwards is

A disc of mass $2\mathrm{ }\mathrm{kg}$ and radius $0.2 \mathrm{m}$ is rotating with an angular velocity $30\mathrm{ }\mathrm{rad} {\mathrm{s}}^{-1}$, about an axis passing through its centre and perpendicular to its plane. If a mass of $0.25\mathrm{ }\mathrm{kg}$ is stuck on the periphery of the disc, then its angular velocity will become

A block of mass 0.1 kg is attached to a cord passing through a hole in a horizontal frictionless horizontal surface as shown in figure. The block is originally revolving at a distance of 0.4 m from the hole, with an angular velocity of 2 rad ${\mathrm{s}}^{-1}$ . The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.2 m. Considering the block to be point mass, calculate the new angular velocity (in rad/s).

A uniform smooth rod (mass $m$ and length $\mathcal{l}$ ) placed on a smooth horizontal floor is hit by a particle (mass $m$) moving on the floor, at a distance $\frac{\mathcal{l}}{4}$ from one end elastically ($e=1$). The distance travelled by the centre of the rod after the collision, when it has completed three revolutions, will be

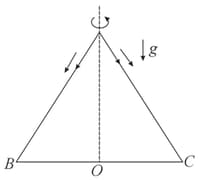
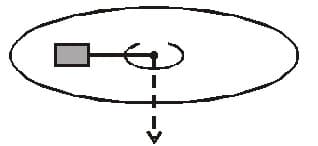
An equilateral triangle ABC formed from a uniform wire has two small identical beads initially located at A. The triangle is set rotating about the vertical axis AO. Then the beads are released from rest simultaneously and allowed to slide down, one along AB and other along AC as shown. Neglecting frictional effects, the quantities that are conserved as beads slides down are