Rolling Motion
Important Questions on Rolling Motion
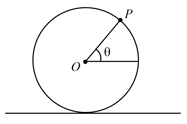
A sphere rolls on the surface with velocity . It encounters a smooth frictionless incline of height which it needs to climb. What will be the minimum velocity for which it will climb the incline?
A disc is in pure rolling motion with a velocity on a rough horizontal surface. The resultant velocity of a point at an angle with the horizontal would be
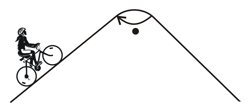
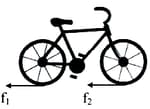
A bicycle is going up on the mountain as shown in the diagram. What can we conclude about the direction of friction?
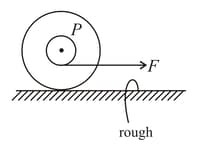
Consider a yo-yo kept vertically on the floor. Its inner and outer radii are , respectively. A thread is wound over its inner surface and placed over a rough horizontal surface. Thread is pulled over by a force . In case of
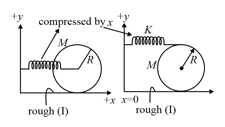
The figure shows two systems in which the spring and sphere remain the same but the connection of spring changes.
Find the ratio of the friction forces in the two cases. (co-ordinate axes are as given)
Consider you are riding a bicycle. Case I:
You are pedalling the cycle and it is rolling on street.
Case II:
You have stopped pedalling and the cycle is still rolling on ground.
Find the product of the dot products of the unit vectors along the direction of friction on the two tyres in the two cases.
A sphere of mass rolls without slipping on a plane inclined at The linear acceleration of the sphere will be The minimum value of for this to be possible is
An object of radius and mass is rolling horizontally without slipping with speed . It then rolls up the hill to a maximum height . The moment of inertia of the object is (acceleration due to gravity)
The ratio of the accelerations for a solid sphere (mass and radius ) rolling down an incline of angle without slipping and slipping down the incline without rolling is
A ring rolls along an inclined plane without slipping. What fraction of the total kinetic energy will be rotational?
The speed of a homogeneous solid sphere after rolling down on an inclined plane of vertical height from rest without sliding is
A uniform round body of radius mass and moment of inertia rolls down (without slipping) on an inclined plane making an angle with the horizontal. The acceleration is
A solid sphere is in a rolling motion. In rolling motion, a body possesses translational kinetic energy as well as rotational kinetic energy simultaneously, The ratio for the sphere is
Three bodies a ring , a solid cylinder and a solid sphere having the same mass and same radius roll down the inclined plane without slipping. They start from rest, if and are velocities of respective bodies on reaching the bottom of the plane, then
A disc and a sphere of the same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first?
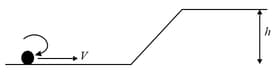
A solid sphere is rolling on a frictionless surface as shown in the figure with a translational velocity . If it is to climb the inclined surface, then should be
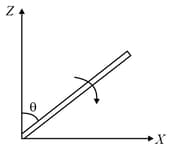
A slender uniform rod of mass and length is pivoted at one end so that it can rotate in a vertical plane (see figure). There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle with the vertical is
An inclined -plane makes an angle of with the horizontal. A solid sphere rolling down this inclined plane from rest without slipping has a linear acceleration equal to
Two identical cylinders are released from the top of two identical inclined planes. If one rolls without slipping and the other slips without rolling, then
A solid sphere is moving on a horizontal plane. Ratio of its translational kinetic energy and rotational kinetic energy is

