Rolling Without Slipping

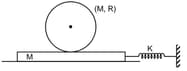
A cylinder of mass $M=2 \mathrm{kg }$and radius $R=12 \mathrm{cm}$ lies on a plank of the same mass as shown in the figure. The surface between plank and ground is smooth but there is friction between cylinder and plank. If the coefficient of friction between the cylinder and the plank is $\mu =0.4$, then what maximum initial compression (in $\mathrm{cm}$) can be given to the spring such that the cylinder moves without slipping with respect to the plank? [Given, $k=200 \mathrm{N} {\mathrm{m}}^{-1}$]

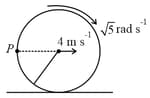
The centre of mass of a disc of radius $\frac{8}{\sqrt{5}} \mathrm{m}$ is moving with a velocity of $4 \mathrm{m} {\mathrm{s}}^{-1}$ on a horizontal plane. The angular velocity of the disc about its centre is $\sqrt{5} \mathrm{rad} {\mathrm{s}}^{-1}$. Find the radius of curvature of the point $P$ shown in the figure (in meter).

For next 2 question please follow the same

A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

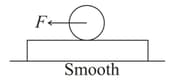
Acceleration of the plank is

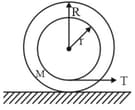
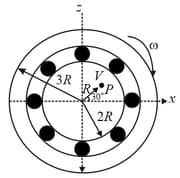
The figure shows a system consisting of$\left(\mathrm{i}\right)$a ring of outer radius $3R$ rolling clockwise without slipping on a horizontal surface with angular speed $\mathrm{\omega }$ and $\left(\mathrm{ii}\right)$ an inner disc of radius $2R$ rotating anti-clockwise with angular speed $\frac{\mathrm{\omega }}{2}.$ The ring and disc are separated frictionless ball bearings. The system is in the $\mathrm{x}-\mathrm{z} \mathrm{plane}.$The point P on the inner disc is at distance $R$ from the origin $\mathrm{O},$ where $\mathrm{OP}$makes an angle of $30º$ with the horizontal. Then with respect to the horizontal surface,

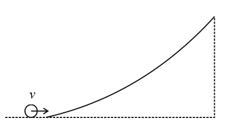
A small object of uniform density rolls up a curved surface with an initial velocity $v$. It reaches up to a maximum height of $\frac{3v^2}{4g}$ with respect to the initial position. The object is 

A uniform solid cylinder rolls without slipping on a rough horizontal floor, its centre of mass moving with a speed $v$. It makes an elastic collision with a smooth vertical wall. After impact

Consider a disc rolling without slipping on a horizontal surface at a linear speed $V$ as shown in the figure

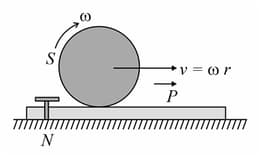
A sphere $S$ rolls without slipping, moving with a constant speed on a plank $P$. The friction between the upper surface of $P$ and the sphere is sufficient to prevent slipping, while the lower surface of $P$ is smooth and rests on the ground. Initially, $P$ is fixed to the ground by a pin $N$. If $N$ is suddenly removed, 

A hollow sphere and a solid sphere having equal mass and equal radii are rolled down without slipping on a rough inclined plane.

A rigid body of radius $R$, either hollow or solid, lies on a smooth horizontal surface. The body is pulled by a horizontal force acting tangentially from the highest point. The distance travelled by the body in the time in which it makes one full rotation is the same, that it will make in one full rotation during pure rolling. The rigid body will be

A spool of mass $M=3 \mathrm{kg}$ and radius $R=20 \mathrm{cm}$ has an axle of radius $r=10 \mathrm{cm}$ around which a string is wrapped. The moment of inertia about an axis perpendicular to the plane of the spool and passing through the centre is $\frac{M{R}^2}{2}$. If the coefficient of friction between the surface and the spool is $0.4$ then the maximum tension which can be applied to the string for which the spool doesn't slip, is $\left[g=10 \mathrm{m} {\mathrm{s}}^{-2}\right]$