Capillarity and Capillary Action

A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is $0°$ and effect to liquid inside the meniscus is to be neglected. $T$ is surface tension of the liquid, $r$ is radius of the meniscus, $g$ is acceleration due to gravity and $p$ is density of the liquid then height h in equilibrium is:

If a capillary of radius $r$ is dipped in water, the height of water that rises in it is $h$ and its mass is $M.$ If the radius. of the capillary is doubled the mass of water that rises in the capillary will be :-

Water rises in a capillary upto a height $h.$ If now this capillary is tilted by an angle of $45°,$ then the length of the water column in the capillary becomes :-

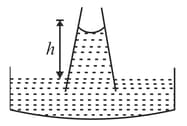
The height to which water rises in a capillary will be :-

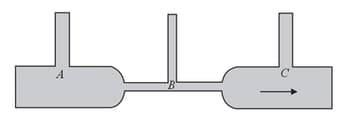
In the figure below is shown the flow of liquid through a horizontal pipe. Three tubes $A,B$ and $C$ are connected to the pipe. The radii of the tubes, $A,B$ and $C$ at the junction are respectively $2 \mathrm{cm},1 \mathrm{cm}$. and $2 \mathrm{cm}$. It can be said that the :-

Water rises to a height of $16.3 \mathrm{cm}$ in a capillary of height $18 \mathrm{cm}$ above the water level. If the tube is cut at a nety $12 \mathrm{cm}$ :-

Water rises to a height $h$ in a capillary at the surface of earth. On the surface of the moon the height of water column in the same capillary will be :-

When a capillary tube is dipped in a liquid, the liquid rises to a height $h$ in the tube. The free liquid surface inside the tube is hemispherical in shape. The tube is now pushed down so that the height of the tube outside the liquid is less than $h :-$

In a capillary tube experiment, a vertical, $30 \mathrm{cm}$ long capillary tube is dipped in water. The water rises upto a height of $10 \mathrm{cm}$ due to capillary action. If this experiment is conducted in a freely falling elevator, the length of the water column becomes

A vessel, whose bottom has round holes with diameter of $0.1 \mathrm{mm}$, is filled with water. The maximum height to which the water can be filled without leakage is (surface tension of water, $T=75 \mathrm{dyne} {\mathrm{cm}}^{-1}$, $g=1000 \mathrm{cm} {\mathrm{s}}^{-2}$)

When a vertical capillary of length $l$, with the sealed upper end, was brought in contact with the surface of a liquid, the level of this liquid rose to the height $h$. The liquid density is $\rho$, the inside diameter of the capillary is $d$, the contact angle is $\mathrm{\theta }$ and the atmospheric pressure is $p_0$. Find the surface tension of the liquid.

On dipping a capillary of radius $r$ in water, the water rises up to a height $H$ and the potential energy of water is $u_1$. If a capillary of the radius $2r$ is dipped in water, then the potential energy is $u_2$. The ratio $\frac{u_1}{u_2}$ is:

Two capillary tubes of the same diameter are put vertically, one each in two liquids whose relative densities are $0.8$ and $0.6$ and surface tensions are $60 \mathrm{dyne} {\mathrm{cm}}^{-1}$and $50 \mathrm{dyne} {\mathrm{cm}}^{-1}$, respectively. Ratio of heights of liquids in the two tubes is,