Standing Waves in Strings and Organ Pipes

In a sonometer wire the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has volume of 0.0075m^​3. The fundamental frequency of the wire is 260Hz. Find the new fundamental frequency if the suspended mass is completely submerged in water

The fundamental frequencies of two copper wire of same length are in the ratio $1:2$. If the tension on the wires are$729 \mathrm{g}$ and $324 \mathrm{g}$ respectively, then the ratio of their diameters will be:

A wire of density $8\times {10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$ is stretched between two clamps $0.5 \mathrm{m}$ apart. The extension developed in the wire is $3.2\times {10}^{-4} \mathrm{m}$. If $Y=8\times {10}^{10} \mathrm{N} {\mathrm{m}}^{-2}$, the fundamental frequency of vibration in the wire will be _____ $\mathrm{Hz}$

A guitar string of length $90 \mathrm{cm}$ vibrates with a fundamental frequency of $120 \mathrm{Hz}$. The length of the string producing a fundamental of $180 \mathrm{Hz}$ will be _____ $\mathrm{cm}$

In an experiment with sonometer when a mass of $180 \mathrm{g}$ is attached to the string, it vibrates with fundamental frequency of $30 \mathrm{Hz}$. When a mass $m$ is attached, the string vibrates with fundamental frequency of $50 \mathrm{Hz}$. The value of $m$ is ______ $\mathrm{g}$.

For a certain organ pipe, the first three resonance frequencies are in the ratio of $1:3:5$ respectively. If the frequency of fifth harmonic is $405 \mathrm{Hz}$ and the speed of sound in air is $324 \mathrm{m} {\mathrm{s}}^{–1}$ the length of the organ pipe is _____ $\mathrm{m}$.

The fundamental frequency of vibration of a string between two rigid support is $50 \mathrm{Hz}$. The mass of the string is $18 \mathrm{g}$ and its linear mass density is $20 \mathrm{g} {\mathrm{m}}^{-1}$. The speed of the transverse waves so produced in the string is _______ $\mathrm{m} {\mathrm{s}}^{–1}$.

An organ pipe $40 \mathrm{cm}$ long is open at both ends. The speed of sound in air is $360 \mathrm{m} {\mathrm{s}}^{-1}$. The frequency of the second harmonic is _$\_\_\_\_\_\_\_\_ \mathrm{Hz}.$

A standing wave $y=A\sin \left(\frac{20\pi x}{3}\right) \cos \left(1000\pi x\right)$is maintained in a taut string where $y$ and $x$ are expressed in meters. The distance between the successive points oscillating with the amplitude$\frac{A}{2}$ across a node is equal to

A $100 \mathrm{cm}$ string fixed at both ends produces successive resonance frequency $384 \mathrm{Hz}$ and $288 \mathrm{Hz}$. Wave speed in string is $24n$ $\mathrm{m} {\mathrm{s}}^{-1}$. Find the value of$n$.

When a tuning fork vibrates with $1.0 \mathrm{m}$ or $1.05 \mathrm{m}$ long wire (both in same mode), $5$ beats per second are produced in each case. If the frequency of the tuning fork is $5f$ (in $Hz$) find$f$.

 An open organ pipe of length $L$ vibrates in second harmonic mode. The pressure vibration is maximum 

When a tuning fork vibrates with $1.0 \mathrm{m}$ or $1.02 \mathrm{m}$ long wire of a sonometer (in fundamental mode), beat frequency observed is $2 \mathrm{Hz}$. Speed of wave in sonometer wire is $24c \mathrm{m} {\mathrm{s}}^{-1}$, then $c$ is

A $100 \mathrm{cm}$ string fixed at both ends produces successive resonance frequency $384 \mathrm{Hz}$ and $288 \mathrm{Hz}$. Wave speed in string is $16P \mathrm{m} {\mathrm{s}}^{-1}$, then$P$ is

Equation of a stationary wave can be expressed as $y=8\sin \frac{\pi x}{4} \cos 20\pi t$ here$x$and $y$ are in cm and$t$ in second, wavelength of any component of  progressive wave is

For an addition of $75 \mathrm{kg} \mathrm{wt}$ to the vibrating string raises the pitch by an octave of the original pitch then tension in string is

In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of $20.0 \mathrm{cm}$ for a tuning fork of frequency $400 \mathrm{Hz}$ is used. The velocity of the sound at room temperature is $336 \mathrm{m} {\mathrm{s}}^{-1}$. The third resonance is observed when the air column has a length of _____ $\mathrm{cm}$

Look at the arrangement

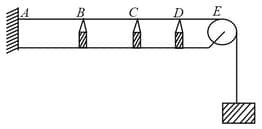
The fundamental frequency corresponding to the part of the string $AB$ is $600\mathrm{Hz}$, the fundamental frequency corresponding to the part $BC$ is $800\mathrm{Hz}$, the fundamental frequency corresponding to the part $CD$ is $1200\mathrm{Hz}$ and the fundamental frequency corresponding to the part $DE$ of the string is $2400\mathrm{Hz}$. If all the wedges are removed and the total string starts vibrating the frequency heard is $1200\mathrm{Hz}$. The string is vibrating in which overtone?

The tones that are separated by three octaves have a frequency ratio of

A steel wire $8\times {10}^{-4} \mathrm{m}$ in diameter is fixed to a support at one end and is wrapped round a cylindrical tuning peg $5 \mathrm{mm}$ in diameter at the other end. The length of the wire between the peg and the support is $0.06 \mathrm{m}$. The wire is initially kept taut but without any tension. If the fundamental frequency of vibration of the wire if it is tightened by giving the peg a quarter of a turn is $1.08\times {10}^{\mathrm{n}}\mathrm{Hz}$. Then find the value of $n$
Density of steel $=7800 \mathrm{kg}/{\mathrm{m}}^3,Y$ of steel $=20\times {10}^{10} {\mathrm{Nm}}^{-2}$.