Simple Harmonic Motion

Electrons moving with different speeds enter a uniform magnetic field in a direction perpendicular field. They will move along circular paths, time periods of rotation will be :

A spring of force constant $200 \mathrm{N} {\mathrm{m}}^{-1}$ is cut into three parts of lengths in ratio $1: 2: 3$. The smallest spring is further cut into two parts of equal length. The force constant of the shortest spring formed will be

The average power transmitted through a given point on a string supporting a sine wave is. $0.40 \mathrm{W}$ when the amplitude of wave is$2 \mathrm{mm}$. What average power will be transmitted through this point if its amplitude is increased to $4 \mathrm{mm}$

At $t=\frac{2T}{3}$ a particle is at $\frac{-A}{2}$ and moving towards mean position. Find the equation of SHM. Also find the speed at $\frac{T}{4}$

A simple pendulum of length $1 \mathrm{m}$ is allowed to oscillate with amplitude $2º$, It collides elastically with a wall inclined at $1°$ to the vertical. Its time period will be (use $g={\pi }^2$ )

A particle performs S.H.M. with amplitude $A$. The speed of particle is doubled at the instant when it is at $\frac{A}{2}$distance from mean position. The new amplitude of the motion is

A body of mass $1 \mathrm{kg}$ falls freely from a height of $100 \mathrm{m}$, on a platform of mass $3 \mathrm{kg}$ which is mounted on a spring having spring constant$k=1.25\times {10}^6 \mathrm{N} {\mathrm{m}}^{-1}$. The body sticks to the platform and the spring's maximum compression is found to be$x$. Given that $g=10 \mathrm{m} {\mathrm{s}}^{-2}$, the value of $x$ will be close to 

A body attached to a spring oscillates in horizontal plane with frequency$n$. Its total energy is $E$ If the velocity in he mean position is$v$, then the spring constant is

Two particles executing SHM of same frequency and same amplitude meet at $x=+\frac{\sqrt{3}A}{2}$while moving in opposite directions. Phase difference between the particles is :-

At a given point of time the value of displacement of a simple harmonic oscillator is given as $y=A \cos \left(30°\right).$ If amplitude is $40 \mathrm{cm}$ and kinetic energy at that time is $200 \mathrm{J},$ the value of force constant $1.0\times {10}^x \mathrm{N} {\mathrm{m}}^{–1}$. The value of $x$ is _____.

A particle executes SHM of amplitude$A$. The distance from the mean position when its kinetic energy becomes equal to its potential energy is:

A particle is executing simple harmonic motion (SHM). The ratio of potential energy and kinetic energy of the particle when its displacement is half of its amplitude will be

Which graph represents the difference between total energy and potential energy of a particle executing $\mathrm{SHM}$ vs its distance from mean position?

In a linear Simple Harmonic Motion (SHM)

(A) Restoring force is directly proportional to the displacement.

(B) The acceleration and displacement are opposite in direction.

(C) The velocity is maximum at mean position.

(D) The acceleration is minimum at extreme points.

Choose the correct answer from the options given below:

The variation of kinetic energy (KE) of a particle executing simple harmonic motion with the displacement ($x$) starting from mean position to extreme position ($A$) is given by

A rectangular block of mass $5 \mathrm{kg}$ attached to a horizontal spiral spring executes simple harmonic motion of amplitude $1 \mathrm{m}$ and time period $3.14 \mathrm{s}$. The maximum force exerted by spring on block is ___ $\mathrm{N}$.

A particle executes S.H.M. of amplitude $A$ along $x$-axis. At $t=0$, the position of the particle is $x=\frac{A}{2}$ and it moves along positive $x$-axis. The displacement of particle in time $t$ is $x=A \sin \left(\omega t + \delta \right)$, then the value $\delta$ will be

A simple pendulum with length $100 \mathrm{cm}$ and bob of mass $250 \mathrm{g}$ is executing S.H.M of amplitude $10 \mathrm{cm}$. The maximum tension in the string is found to be $\frac{x}{40} \mathrm{N}$. The value of $x$ is _____.(to the nearest integer)

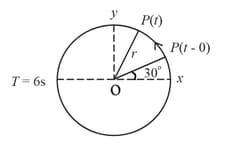
For particle $P$ revolving round the centre $O$ with radius of circular path $r$ and regular velocity $\omega$, as shown in below figure, the projection of $OP$ on the $x$-axis at time $t$ is

For a periodic motion represented by the equation $y=\mathrm{sin\omega }t+\mathrm{cos\omega }t$ the amplitude of the motion is