Oscillations of Spring Mass System

For two masses attached to a spring as shown in the diagram, prove that the effective inertial mass of the system is given by

$\mu =\frac{m_1{m}_2}{m_1+m_2}$

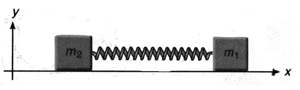
In which one of the following cases for two masses $m_1$ and $m_2$ is/are correct for their effective inertial mass $\mu$?

For two masses $m_1$ and $m_2$ connected at both the ends of a spring, which one of the following relation is correct for their reduced mass?

Two identical blocks of mass $m$ are connected via a spring of spring constant $k$ as shown in the diagram

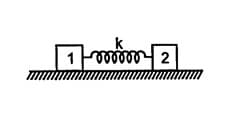
The time period of the system when both are given a small displacement in opposite directions will be

A light spring of force constant $8 {\mathrm{Nm}}^{-1}$ is cut into two equal halves and the two are connected in parallel; the equivalent force constant of the system is

A light spring of constant $k$ is cut into two equal parts. The spring constant of each part is

In a spring-mass system, the length of the spring is $L$, and it has a mass $M$ attached to it and oscillates with an angular frequency $\omega$. The spring is then cut into two parts, one (a) with relaxed length $\alpha L$and the other (b) with relaxed length $\left(1-\alpha \right)L$. The force constants of the two springs $A$ and $B$ are

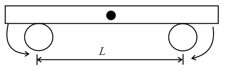
A uniform plate of mass $\mathrm{M}$ stays horizontally and symmetrically on two wheels rotating in opposite directions shown in figure. The separation between the wheels is $\mathrm{L}$. The friction coefficient between each wheel and the plate is $\mu$ . Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

Match the Column I with Column II:

	Column - I		Column - II
$\left(\mathrm{a}\right)$		$\left(\mathrm{i}\right)$	$T=2\mathrm{\pi }\sqrt{\frac{m\left(k_1+k_2\right)}{k_1{k}_2}}$
$\left(\mathrm{b}\right)$		$\left(\mathrm{i}\mathrm{i}\right)$	$T=2\mathrm{\pi }\sqrt{\frac{2\mathit{ }m}{k}}$
$\left(\mathrm{c}\right)$		$\left(\mathrm{i}\mathrm{i}\mathrm{i}\right)$	$T=2\mathrm{\pi }\sqrt{\frac{m}{2\mathit{ }k}}$
$\left(\mathrm{d}\right)$		$\left(\mathrm{i}\mathrm{v}\right)$	$T=2\mathrm{\pi }\sqrt{\frac{m}{k_1+k_2}}$

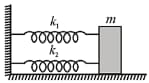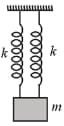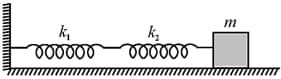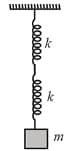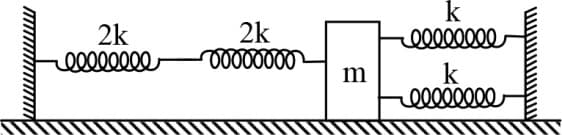
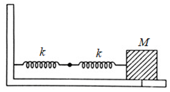
A trolley of mass $3\mathrm{ }\mathrm{k}\mathrm{g}$, as shown in figure, is connected to two identical springs, each having spring constant equal to $600\mathrm{ }\mathrm{N} {\mathrm{m}}^{-1}$. If the trolley is displaced from its equilibrium position by $5\mathrm{ }\mathrm{c}\mathrm{m}$ and released, the maximum speed of the trolley is:

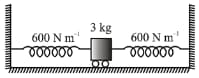
Two springs are connected to a block of mass $M$ placed on a frictionless surface as shown below. If both the springs have a spring constant $k,$ then the frequency of oscillation of the block is

As shown in figure a simple harmonic motion oscillator having identical four springs has time period

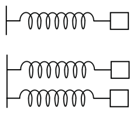
If ${\mathrm{k}}_{\mathrm{s}}$ and ${\mathrm{k}}_{\mathrm{p}}$ respectively are effective spring constant in series and parallel combination of springs as shown in figure, find $\frac{{\mathrm{k}}_{\mathrm{s}}}{{\mathrm{k}}_{\mathrm{p}}}$

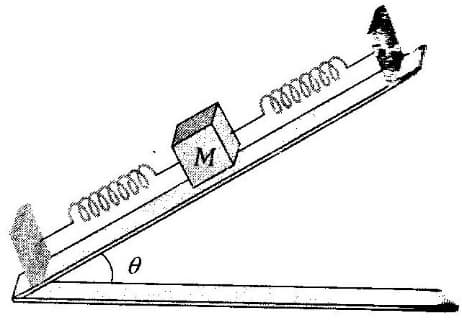
On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K, the period of oscillation of the body (assuming the springs as massless) is

A spring of force constant k is cut into two pieces such that one piece is double the length of the other. Then the long piece will have a force constant of

A particle at the end of a spring executes simple harmonic motion with a period ${\mathrm{t}}_1$ , while the corresponding period for another spring is ${\mathrm{t}}_2$ . If the period of oscillation with the two springs in series is $\mathrm{T}$ , then -

A particle at the end of a spring executes simple harmonic motion with a period ${\mathrm{t}}_1$ , while the corresponding period for another spring is ${\mathrm{t}}_2$ . If the period of oscillation with the two springs in series is $\mathrm{T}$ , then -

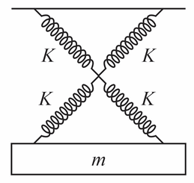
Four spring connect with mass as shown in figure. Find frequency of S.H.M.

The time period of a mass suspended from a spring is $5 \mathrm{s}$. The spring is cut into four equal parts and the same mass is now suspended from one of its parts. The period is now

A mass $\mathrm{m}$ is attached to four springs of spring constants $2\mathrm{k},\mathrm{ }2\mathrm{k},\mathrm{ }\mathrm{k}, \mathrm{k}$ as shown in figure. The mass is capable of oscillating on a frictionless horizontal floor. If it is displaced slightly and released the frequency of resulting $\mathrm{S}\mathrm{H}\mathrm{M}$ would be -