Oscillations of a Spring - Block System

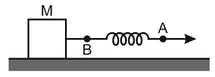
A block of mass $\mathrm{M}$ is placed on a smooth horizontal surface, and it is pulled by a light spring as shown in the diagram. If the ends $\mathrm{A}$ and $\mathrm{B}$ of the spring are moving with $4 \mathrm{m} {\mathrm{s}}^{-1}$ and $2 \mathrm{m} {\mathrm{s}}^{-1}$ respectively in the same direction and at this moment the rate at which spring energy is increasing is $20 \mathrm{J} {\mathrm{s}}^{-1}$, then what is the value of spring force (in $\mathrm{N}$)?

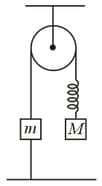
A mass of $0.2 \mathrm{kg}$ is attached to the lower end of a massless spring of force constant $200 \mathrm{N} {\mathrm{m}}^{-1}$, the upper end of which is fixed to a rigid support. Which of the following statement is true?

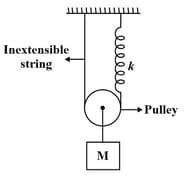
An arrangement of spring, strings, pulley and masses is shown in the figure below.

The pulley and the strings are massless and $M>m$. The spring is light with spring constant $k$. If the string connecting $m$ to the ground is detached, then immediately after detachment

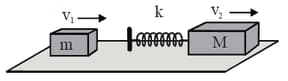
Two blocks of masses $m$ and $M$ are moving with speed $v_1$ and $v_2\left(v_1>v_2\right)$ in the same direction on the frictionless surface respectively, $M$ being ahead of $m$. An ideal spring of force constant $k$ is attached to the backside of $M$ (as shown). The maximum compression of the spring when the blocks collide is 

Angular frequency in SHM is given by $\text{ω}=\sqrt{\frac{\text{k}}{\text{m}}}$. Maximum acceleration in SHM is ${\text{ω}}^{2}A$ and maximum value of friction between two bodies in contact is $\text{μ}\text{N}$, where N is the normal reaction between the bodies.
  Now the value of k, the force constant is increased, then the maximum amplitude calculated in above question will

Electrostatic force on a charged particle is given by $\overrightarrow{\text{F}}=\text{q}\overrightarrow{\text{E}}$. If q is positive $\overrightarrow{\text{F}}\uparrow \uparrow \overrightarrow{\text{E}}$ and if q negative $\overrightarrow{\text{F}}\uparrow \downarrow \overrightarrow{\text{E}}$

In the figure m_A = m_B = 1 kg. Block A is neutral while q_B = - 1C. Sizes of A and B are negligible. B is released from rest at a distance 1.8 m from A. Initially  spring is neither compressed nor elongated.

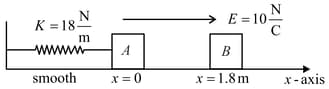
Equilibrium position of the combined mass is at $x = ........m$

Statement 1: Acceleration must be proportional to displacement and directed towards mean position in a simple harmonic motion.

Statement 2: A mass $\mathrm{M}$ is suspended from vertical spring of some force constant and the equation of motion is $\mathrm{My}=-\mathrm{ky}+\mathrm{Mg}$as shown in the Figure, then it shows that motion is not simple harmonic unless $\mathrm{Mg}$ is negligibly small.

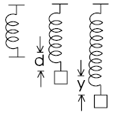
Let $k$ be the spring constant of a spring. If the spring is cut into two equal parts, then spring constant of each part is

A spring with a spring constant $1200 \mathrm{N} {\mathrm{m}}^{-1}$ is mounted on a horizontal table as shown. A mass of $3 \mathrm{kg}$ is attached to the free end of the spring. Then the mass is pulled sideways to a distance of $2.0 \mathrm{cm}$ and released. If the maximum acceleration of the mass and the maximum speed of the mass is $x \mathrm{m} {\mathrm{s}}^{-2} \text{and} y \mathrm{m} {\mathrm{s}}^{-1}$ respectively. Then the value of $\left(x+y\right)$ is:

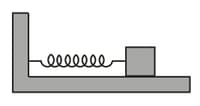
The time period of mass $M$ when displaced from its equilibrium position and then released for the system as shown in figure is

A spring balance has a scale that reads from $0$ to $50\mathrm{ }\mathrm{k}\mathrm{g}$. The length of the scale is $20\mathrm{ }\mathrm{c}\mathrm{m}$. A block of mass $\mathrm{m}$ is suspended from this balance, displaced from its mean position and released, it oscillates with a period $0.5\mathrm{ }\mathrm{s}$. The value of $\mathrm{m}$ is (Take $g=10\mathrm{ }\mathrm{m} {\mathrm{s}}^{-2}$)

Two blocks each of mass $m$, kept on smooth surface, are connected by a spring of spring constant $k$ as shown in the figure.

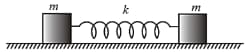
If the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. The time period of oscillation is

Natural length of the spring is $40\mathrm{ }\mathrm{c}\mathrm{m}$ and its spring constant is $4000\mathrm{ }\mathrm{N}\mathrm{ }{\mathrm{m}}^{-1}.$ A mass of $20\mathrm{ }\mathrm{k}\mathrm{g}$ is hung from it. The extension produced in the spring is
(Given $\mathrm{ }\mathrm{g}\mathrm{ }=9.8\mathrm{ }\mathrm{m}\mathrm{ }{\mathrm{s}}^{-2}$ )

The minimum time taken by a spring block system (having time period T) to travel a distance equal to amplitude of motion is equal to

A particle, at the end of a spring, executes simple harmonic motion with a period $t_1$, while the corresponding period, for another spring, is $t_2$. If the period of oscillation with the two springs in series is $T$, then

A mass on the end of a spring undergoes simple harmonic motion with a frequency of 0.5 Hz. If the attached mass is reduced to one quarter of its value, then the new frequency in Hz is

A particle of mass m is attached to three identical springs A, B and C each of force constant k a shown in figure. If the particle of mass m is pushed slightly against the spring A and released then the time period of oscillations is

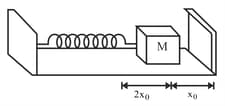
One end of a spring of force constant k is fixed to a vertical wall and the other to a block of mass m resting on a smooth horizontal surface. There is another wall at a distance $x_0$ from the block. The spring is then compressed by $2x_0$ and released. The time taken to strike the wall is

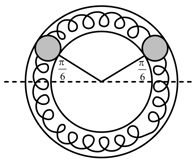
Two identical balls A and B each of mass 0.1 kg are attached to two identical massless springs. The spring mass system is constrained to move inside a rigid smooth pipe of bent in the form of a circle as shown in the figure. The pipe is fixed in a horizontal plane. The centers of the balls can move in a circle of radius 0.06m. Each spring has a natural length of $0.06\pi m$ and force constant $0.1\frac{N}{m}$ . Initially both the balls are displaced by an angle $\theta =\frac{\pi }{6}$ radian with respect to the diameter PQ of the circle and released from rest. The frequency of oscillation of the ball B is

An ideal spring with spring-constant $K$is hung from the ceiling and a block of mass $M$ is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is