Oscillations of a Spring - Block System

Let $k$ be the spring constant of a spring. If the spring is cut into two equal parts, then spring constant of each part is

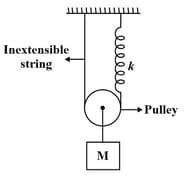
The time period of mass $M$ when displaced from its equilibrium position and then released for the system as shown in figure is

A spring balance has a scale that reads from $0$ to $50\mathrm{ }\mathrm{k}\mathrm{g}$. The length of the scale is $20\mathrm{ }\mathrm{c}\mathrm{m}$. A block of mass $\mathrm{m}$ is suspended from this balance, displaced from its mean position and released, it oscillates with a period $0.5\mathrm{ }\mathrm{s}$. The value of $\mathrm{m}$ is (Take $g=10\mathrm{ }\mathrm{m} {\mathrm{s}}^{-2}$)

Two blocks each of mass $m$, kept on smooth surface, are connected by a spring of spring constant $k$ as shown in the figure.

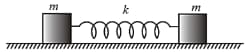
If the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. The time period of oscillation is

Natural length of the spring is $40\mathrm{ }\mathrm{c}\mathrm{m}$ and its spring constant is $4000\mathrm{ }\mathrm{N}\mathrm{ }{\mathrm{m}}^{-1}.$ A mass of $20\mathrm{ }\mathrm{k}\mathrm{g}$ is hung from it. The extension produced in the spring is
(Given $\mathrm{ }\mathrm{g}\mathrm{ }=9.8\mathrm{ }\mathrm{m}\mathrm{ }{\mathrm{s}}^{-2}$ )

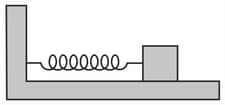
A spring having a spring constant of $1200 \mathrm{N} {\mathrm{m}}^{-1}$, is mounted on a horizontal table, as shown in the figure. A mass of $3 \mathrm{kg}$ is attached to the free end of the spring. Then, the mass is pulled sideways to a distance of $2.0 \mathrm{cm}$ and released. Determine the maximum acceleration of the mass, and the maximum speed of the mass.

​​​​​​​

A solid copper sphere is suspended from a massless spring. The time period of oscillation of the system is 4 second. The sphere is now completely immersed in a liquid whose density is 1/8 th that of brass. The sphere remains in liquid during oscillation. Now the time period is