Equation of SHM

The $\mathrm{x}-\mathrm{t}$ graph of a particle undergoing simple harmonic motion is as shown in the figure.

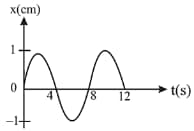
The acceleration of the particle at $\mathrm{t}=\frac{4}{3}\mathrm{ }\mathrm{s}$ is

Which one of the following expressions does not represent simple harmonic motion (SMH)?

The phase difference between the displacement and velocity of a particle executing simple harmonic motion is

What will be the initial phase of simple harmonic motion represented by the equation $x=A\sin \left(\omega t\right)+B\cos \left(\omega t\right)$.

If two SHMs of different amplitudes are added together, the resultant SHM will be a maximum if the phase difference between them is:

Two particles execute simple harmonic motions of same amplitude and frequency along the same straight line. They cross one another when going opposite directions. The phase difference between them when their displacements are one half of their amplitudes is then:

Graph between velocity and displacement of a particle, executing S.H.M. is

Initial phase of the particle executing SHM with $y=4\sin \omega t+3\cos \omega t$ is:

When two particles executing SHM are overlapped in opposite phase then resultant amplitude will be 

The displacement of two particles executing SHM are expressed as ${\mathrm{y}}_1=\mathrm{a} \sin \left(\mathrm{\pi t}+\mathrm{\varphi }\right)$ and ${\mathrm{y}}_2=\mathrm{b} \sin \left(2\mathrm{\pi t}+\mathrm{\varphi }\right)$ then at $\mathrm{t}=1 \sec$ both are

Two simple harmonic motions have displacements ${\mathrm{x}}_1=12 \sin \left(\mathrm{\omega t}+\raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)$ and ${\mathrm{x}}_2=6 \sin \left(\mathrm{\omega t}+\raisebox{1ex}{$3\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)$ are superimposed on each other. Resulting amplitude will be.

Two SHM’s are respectively by $y=a_1\sin (\omega t-kx)$ and $y=a_2\cos (\omega t-kx).$ The phase difference between the two is

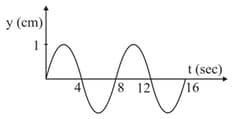
The figure below shows the displacement vs time plot of a particle undergoing simple harmonic motion. The acceleration of the particle at time $t=\frac{4}{3}$ sec would be

Suppose a particle P is moving uniformly on a circle of radius A with the angular speed $\omega$ . The sense of rotation is anticlockwise. If the $t=0$ , it  makes an angle of $\varphi$ with the positive direction of the x-axis. In time $t$, it will cover a further angle $\omega t$.What is the projection of position vector on the X-axis at time $t$.

If we tie a stone to the end of a string and move it with a constant angular speed in a horizontal plane about fixed point, the stone would perform a : 

If the particle is moving in circular motion under SHM, then its x-projection is depending upon

The x-projection for a certain particle in circular motion under SHM with period of $2 \mathrm{s}$, amplitude of oscillation is $2 \mathrm{m}$ and initial phase of $\frac{\mathrm{\pi }}{2}$ is

The displacement equation of a particle is $x=3\sin 2t+4\cos 2t$. The amplitude and maximum velocity will be respectively

A particle performs $\mathrm{S}\text{.}\mathrm{H}\text{.}\mathrm{M}\text{.}$ on $x-$axis with amplitude $A$ and time period $T.$ The time taken by the particle to travel a distance $\frac{A}{5}$ starting from rest is :

Two $\mathrm{SHM}$(simple harmonic motion) are represented by equations, $y_1=6 \cos \left(6\pi t+\frac{\pi }{6}\right), y_2=3 \left(\sqrt{3}\sin 3\pi t+\cos 3\pi t\right)$