Force and Energy Method in SHM

The ratio of kinetic energy at a mean position to potential energy at $\frac{A}{2}$ of a particle performing $\mathrm{SHM}$ is

$U$ is the potential energy of an oscillating(SHM) particle and $F$ is the force acting on it at a given instant. Which of the following is correct?

(Given $x$ is displacement of the particle)

The drawing shows a top view of a frictionless horizontal surface, where there are two springs with particles of mass $m_1$ and $m_2$ attached to them. Each spring has a spring constant of $1200$ $\mathrm{N}/\mathrm{m}$. The particles are pulled to the right and then released from the positions shown in the drawing. How much time passes before the at $x=0$ $\mathrm{m}$ if $m_1=3$ $\mathrm{kg}$ and $m_2=27$ $\mathrm{kg}$. If time is $\frac{n\pi }{80}$ $\sec$, fill $n$ in OMR sheet.

There is a cylindrical bottle of negligible mass and radius $2.5 \mathrm{c}\mathrm{m}$ floating in the water of density ${10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$ filled with $310 \mathrm{m}\mathrm{l}$ of water inside it. Now the bottle is slightly dipped into water and released. The frequency of oscillation is

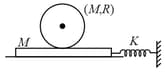
A cylinder of mass $\mathrm{M}$ and radius $\mathrm{R}$ lies on a plank of mass $\mathrm{M}$ as shown. The surface between plank and ground is smooth, and between cylinder and plank is rough. Assuming no slipping between cylinder and plank, the time period of oscillations (when displaced from equilibrium) of the system is

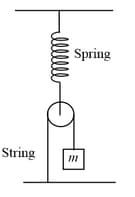
Find the period of low amplitude vertical vibrations of the system shown The mass of the block is m. The pulley hangs from the ceiling on a spring with a force constant k. The block hangs from an ideal spring.

A particle of mass 5 x 10^-5 kg is placed at the lowest point of a smooth parabola having the equation x² = 40y (x, y in cm). If it is displaced slightly and it moves such that it is constrained to move along the parabola, the angular frequency of oscillation will be, approximately

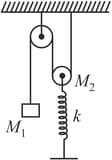
A block of mass ${\mathrm{M}}_1$ is constrained to move along with a moveable pulley of mass ${\mathrm{M}}_2$ which is connected to a spring of force constant $\mathrm{k}$, as shown in the figure. If the mass of the fixed pulley is negligible and friction is absent everywhere, then the period of small oscillations of the system is