Oscillating Systems

A wooden cylinder of mass $20 \mathrm{g}$ and area of cross-section $1 {\mathrm{cm}}^2$, having a piece of Lead of mass $60 \mathrm{g}$ attached to its bottom, floats in water. The cylinder is depressed and then released. Find the frequency of oscillations.

A rectangular block of mass $m$ and area of cross-section $A$ floats in a liquid of density $\rho$. If it is given a small vertical displacement from equilibrium position it undergoes oscillations with a time period $T$. Then

A simple pendulum suspended from the roof of a lift oscillates with frequency $f$ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes:

(Write the answer in numericals)

What will be the time period of the pendulum of length l suspended from the ceiling of a cart which is sliding without friction on an inclined plane of inclination θ ?

An U tube of uniform bore of cross-sectional area A is set up vertically with open ends up. A liquid of mass M and density d is poured into it and allowed to oscillate.Then liquid column will oscillate with a time period-

A rectangular block of mass $m$ and area of cross-section $A$ floats in a liquid of density $\rho$. If it is given a small vertical displacement from equilibrium position it undergoes oscillations with a time period $T$. Then

A wooden cylinder of mass $20 \mathrm{g}$ and area of cross-section $\mathrm{1\hspace{0.17em}}{\mathrm{cm}}^2$, having a piece of lead of mass $60\mathrm{\hspace{0.17em}}\mathrm{g}$ attached to its bottom, floats in water. The cylinder is depressed and then released. The frequency of oscillations is  $\frac{N}{4\pi } {\mathrm{s}}^{-1}$. Find the value of $N$. [Neglect the volume of water displaced by the lead piece, take $g=9.8\mathrm{\hspace{0.17em}}\mathrm{m} {\mathrm{s}}^{-2}$, density of water ${\rho }_{\mathrm{w}}=1 \mathrm{g} {\mathrm{cm}}^{-3}$]

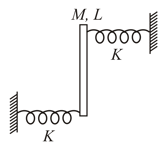
A rod of length $\mathcal{l},$ mass m are connected to two springs of spring constant $K$ each. Find the frequency of small oscillation

The time-period of a simple pendulum of length $\sqrt{5} \mathrm{m}$ suspended in a car moving with uniform acceleration of $5 \mathrm{m }{\mathrm{s}}^{-2}$ in a horizontal straight road is $\left(g=10 \mathrm{m }{\mathrm{s}}^{-2}\right)$

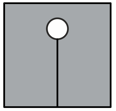
A cork suspended from the bottom of a container filled with water with a string as shown in figure. If the container accelerates in a horizontal direction towards right with an acceleration 'a', which one of the following statements is correct?

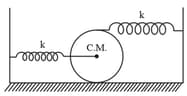
A uniform solid cylinder can roll without sliding on a horizontal surface as shown in the figure. The mass of cylinder is $10 \mathrm{kg}$ and the spring constant for both the ideal springs is $300 \mathrm{N} {\mathrm{m}}^{-1}$. What is the angular frequency (in $\mathrm{rad} {\mathrm{s}}^{-1}$) of small oscillations of the centre of the cylinder?

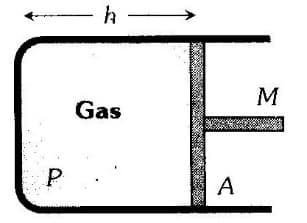
A cylindrical piston of mass M slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of gas. The cylinder is kept with its axis horizontal. If the piston is disturbed from its equilibrium position, it oscillates simple harmonically. The period of oscillation will be

The period of oscillation of a simple pendulum of length $l$ suspended from the roof of a vehicle which moves without friction down an inclined plane of inclination $\alpha$ is given by

A bottle weighing 220 g and of area of cross-section 50 cm2 and height 4 cm oscillates on the surface of water in vertical position. Its frequency of oscillation is

A simple pendulum of length $l$ has been set up inside a railway wagon sliding down a frictionless inclined plane having an angle of inclination $\mathrm{\theta }={30}^0$ with the horizontal. What will be its period of oscillation as recorded by an observer inside the wagon?

A tunnel is made across the earth of radius $R$, passing through its centre. A ball is dropped from a height h in the tunnel. The motion will be periodic with time period.

A simple pendulum is suspended from the ceiling of a lift. When the lift is at rest its time period is $T$. With what acceleration should the lift be accelerated upwards in order to reduce its period to $\frac{T}{2}$? ($g$ is acceleration due to gravity)

A wooden cube (density of wood $d$) of slide $l$ floats in a liquid of density $\mathrm{\rho }$ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonics motion of period $T$, then $T$ is equal

The period of a simple pendulum inside a stationary lift is $T$. The lift accelerates upwards with an acceleration of $g/3$. The time period of pendulum will be

What is time period of pendulum hanged in satellite?

($T$ is time period on earth)