Formation of Standing Waves in an Air Column
Formation of Standing Waves in an Air Column: Overview
This topic covers concepts, such as Kundt's Tube, Organ Pipes, Open Organ Pipe, Fundamental Frequency of Open Organ Pipe, Harmonics and Overtones in Open Organ Pipe, Pressure Wave in Open Organ Pipe, Closed Organ Pipe, etc.
Important Questions on Formation of Standing Waves in an Air Column
In a resonance tube water is filled so that height of air column is when it resonates in its fundamental mode. Now water is removed so that the height of air column becomes and it resonates with next higher frequency. Then end correction is :-
The ratio of first harmonic of open organ pipe and closed organ pipe for the same length is
fundamental frequency of closed organ pipe is ( velocity of sound in air, Length of organ pipe)
Fundamental frequency of open organ pipe is ( Velocity of sound in air, Length of pipe)
For a organ pipe of length , closed at both ends, the first displacement node is presend at :
As an empty vessel is filled with water, its frequency:
An open pipe of length resonates with frequency of . If the speed of sound is , then this frequency is:
An organ pipe closed at one end vibrating in its first overtone and another pipe open at both ends vibrating in its third overtone are in resonance with a given tuning fork. The ratio of the length of to that of is:
A closed organ pipe of length and an open organ pipe contain gases of densities respectively. The compressibility of gases is same in both the pipes which are vibrating in their first overtone with same frequency. The length of the open organ pipe is:
Tube has both ends open while tube has one end closed. Otherwise, they are identical. The ratio of fundamental frequency of tube and is,
A resonance pipe is open at both ends and of its length is in resonance with an external frequency . If the speed of sound is , which harmonic is in resonance?
The second overtone of an open pipe is in resonance with the first overtone of a closed pipe of length 2m. length of the open pipe is
A closed pipe is suddenly opened and changed to an open pipe of same length. The fundamental frequency of the resulting open pipe is less than that of harmonic of the earlier closed pipe by . Then, the value of fundamental frequency of the closed pipe is
In a resonance tube the first resonance with a tuning fork occurs at and second at . If the velocity of sound is , the frequency of tuning fork is
A closed organ pipe and an open organ pipe of the same length produce beats, when they are set into vibrations simultaneously in their fundamental mode. The length of the open organ pipe is now halved and of closed organ pipe is doubled. The number of beats produced will be,
In a closed organ pipe, the harmonics that are present are:
In an open organ pipe, the harmonics that are missing are:
A pipe open at both ends produces a note of frequency . When the pipe is kept with of its length in water, it produced a note of frequency . The ratio is
An open pipe of sufficient length is dipping in water with a speed vertically. If at any instant is length of tube above water. Then the rate at which fundamental frequency of pipe changes, is (speed of sound )
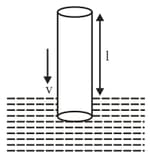
A cylindrical tube open at both ends, has a fundamental frequency in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now
