Power Transmitted by a Wave on a String
Power Transmitted by a Wave on a String: Overview
This topic covers concepts such as Energy and Momentum in Waves, Power Required to Maintain Waves, Intensity of Waves, Kinetic Energy of a Particle in a Sinusoidal Wave, Potential Energy of a Particle in a Wave, etc.
Important Questions on Power Transmitted by a Wave on a String
For a wave, , time-average of kinetic energy is given by:
The kinetic energy of pulse (in ) travelling in a taut string is Given Find the value of
The clocktower ("ghantaghar") of Dehradun is famous for the sound of its bell, which can be heard, albeit faintly, upto the outskirts of the city away. Let the intensity of this faint sound be The clock is situated high. The intensity at the base of the tower is:-
A sensor is exposed for time to a lamp of power placed at a distance . The sensor has a circular opening that is in diameter. Assuming all energy of the lamp is given off as light, the number of photons entering the sensor if the wavelength of light is is :-
A longitudinal standing wave, is maintained in a homogeneous medium of density . Here is the angular speed and k, the wave number and a is the amplitude of the standing wave. This standing wave exists all over a given region of space.
If a graph E (= EP + EK) versus t, (i.e.,) total space energy density versus time were drawn at the instants of time t = 0 and , between two successive nodes separated by distance which of the following graphs correctly shows the total energy (E) distribution at the two instants.
A longitudinal standing wave, is maintained in a homogeneous medium of density . Here is the angular speed and k, the wave number and a is the amplitude of the standing wave. This standing wave exists all over a given region of space.
The space density of the kinetic energy K.E = EK (x, t) at the point (x, t) is given by
For next three question please follow the same
A longitudinal standing wave, is maintained in a homogeneous medium of density . Here is the angular speed and k, the wave number and a is the amplitude of the standing wave. This standing wave exists all over a given region of space.
The space density of the potential energy P.E.= EP (x, t) at a point (x, t) in the space is
In order to have half the velocity in the second case than in the first case, the potential applied should be
If A is the amplitude of the wave coming from a line source at a distance r, then
With the propagation of a longitudinal wave through a material medium, the quantities transmitted in the propagation direction are
A simple harmonic oscillator of frequency is attached to the end of a cord that has a linear mass density and is under a tension . The power that must be provided to the cord by the oscillator to generate a sinusoidal wave of amplitude angular frequency and velocity is
The ends of a stretched wire of length L are fixed at and . In one experiment the displacement of the wire is and energy is and in other experiment its displacement is and energy is .
Then:
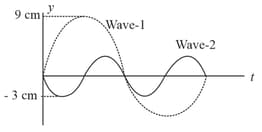
Displacement-time graphs for two waves, wave-1 and wave-2 are shown here. Ratio of intensity of wave-1 to that of wave-2 is
A point source is emitting sound in all directions. The ratio of distance of two points from the point source where the difference in loudness levels is
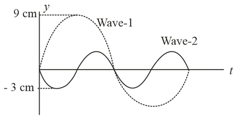
Displacement-time graphs for two waves, wave-1 and wave-2 are shown here. Ratio of intensity of wave-1 to that of wave-2 is
A point source emits sound equally in all direction in a non-absorbing medium. Two points P and Q are at distance of 2 and 3 m respectively from the source. The ratio of the intensities of the wave at P and Q is.
The amplitude of two waves are in ratio . If all other conditions for the two waves are same, then what is the ratio of their energy densities?
The equation of a cylindrical progressive wave is
A stationary point source of sound emits sound uniformly in all directions in a non-absorbing medium. Two points and are at a distance of and , respectively from the source. The ratio of amplitudes of the waves at and is
In a grease spot photometer, light from a lamp with dirty chimney is exactly balanced by a point source distance 10 cm from the grease spot. On clearing the dirty chimney, the point source is moved 2 cm to obtain a balance again. Then the percentage of light absorbed by the dirty chimney is nearly
