Standing Waves on a String

The frequency of a sonometer wire is $f$, but when the weight producing the tensions are completely immersed in water the frequency becomes $\frac{f}{2}$ and on immersing the weights in a certain liquid the frequency becomes $\frac{f}{3}$. The specific gravity of the liquid is

In a sonometer wire the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has volume of 0.0075m^​3. The fundamental frequency of the wire is 260Hz. Find the new fundamental frequency if the suspended mass is completely submerged in water

A string of length $1.5 \mathrm{m}$ with its two ends clamped is vibrating in the fundamental mode. The amplitude at the centre of the string is $4 \mathrm{mm}$. The minimum distance between the two points having amplitude of $2 \mathrm{mm}$ is:

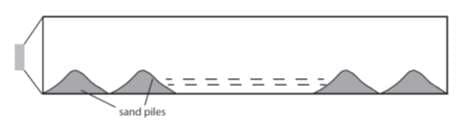
A closed pipe of length $300 \mathrm{cm}$ contains some sand. A speaker is connected at one of its ends. The frequency of the speaker at which the sand will arrange itself in $20$ equidistant piles is close to (velocity of sound is $300 \mathrm{m} {\mathrm{s}}^{-1}$)

The fundamental frequency of a string is proportional to.

On which principle does sonometer work?

In stationary waves, nodes are the points where there is:

A string is vibrating in its fifth overtone between two rigid supports 2.4 $\mathrm{m}$ apart. The distance between successive node and antinode is

In sonometer experiment, the string of length $L$ under tension vibrates in second overtone between two bridges. The amplitude of vibration is maximum at

For the stationary wave $y=4\sin \left(\frac{\pi x}{15}\right)\cos \left(96\mathrm{ }\pi t\right)$ , the distance between a node and the next antinode is

A travelling wave represented by $y=A\sin (\omega t-kx)$ is superimposed on another wave represented by $y=A\sin (\omega t+kx)$. The resultant is:

A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by, $y\left(x, t\right)=0.5\sin \left(\frac{5\pi }{4}x\right)\cos \left(200\pi t\right)$. What is the speed of the travelling wave moving in the positive $x$ direction? ($x$ and $t$are in meter and second, respectively)

In stationary waves, nodes are the points where there is:

A tuning fork having a frequency of $\text{170 Hz}$ is vibrating just above a cylindrical tube. The height of the tube is $\text{110 cm}$. Water is slowly poured in it. What is the minimum height (in $\text{cm}$) of water column required for resonance to occur? (Velocity of sound in air = ${\text{340 m s}}^{-1}$)

Two wires made of same material having radii $r$ (left wire) and $2r$ (right wire) are welded together end to end. This combination is used as a sonometer wire kept under tension $T$. The welded point is midway between the two bridges. What would be the ratio of the number of loops formed in the right wire to the left wire such that the joint is a node when stationary waves are set up in the wires?

A string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is $100 Hz$. The frequency emitted when it vibrates in the next mode such that this point is again a point of maximum displacement is $\eta \times 100 \mathrm{Hz}$. Find the value of $\eta$.

A wire of density $9\times {10}^3 \mathrm{kg}{ \mathrm{cm}}^{-3}$ is stretched between two clamps $1 \mathrm{m}$ apart. The resulting strain in the wire is $4.9\times {10}^{-4}.$ The lowest frequency (in $\mathrm{Hz}$) of the transverse vibrations in the wire is (Young's modulus of wire $\mathrm{Y}=9\times {10}^{10} {\mathrm{Nm}}^{-2}$), (to the nearest integer), _______.

A standing wave is produced on a string fixed at one end and free at other. The length of string must be an _____.

A frequency of a sonometer wire is $100 \mathrm{Hz}$. When, after making length of its wire twice, the tension is increased, then its frequency becomes $75 Hz$. The ratio of its initial and final tension is:

The equation of a standing wave is $y=2a \sin \left(100t\right) \cos \left(0.1x\right)$, where $y$, a are in $\mathrm{mm}$, $t$ in second and $x$ in metre. The velocity of the progressive waves producing it is: