Geometrical Shapes
Geometrical Shapes: Overview
This topic briefs on the different types of geometrical shapes. We will learn the basic terminologies, important properties and formulas of geometrical shapes. It consists of questions that will aid us in revising the concept.
Important Questions on Geometrical Shapes
The amount of space occupied by a three dimensional objects is called its_______?
The line passing through the points and ?
If a square ABCD is inscribed in a circle and AB =., then the radius of circle is-
The wheel of a motor car makes Resolutions in moving . The diameter (in meter) of the wheel is -
A polygon with minimum number of sides is:
If the length of a chord of a circle at a distance of cm from the centre is cm, then the diameter of the circle is-
One chord of a circle is known to be . The radius of this circle must be:
The equation of a straight line passing through the intersection of the lines , and through the point .
In the given figure is the Centre of a circle . Find the radius of the circle?
If the circumcentre of a triangle lie on the side whose adjacent angles are each, then find the other two sides if the radius of the circumcircle is ?
In gradient-intercept form of equation , the denotes:
In the gradient-intercept form of equation , the point where line cuts -axis is:
Which of the following is pair of opposite sides in the given figure.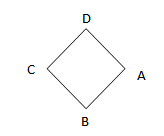
AB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If angle BCD , then angle AOD = ?
Two lines meeting at a point are called ___________ .
If two concentric circles are of radii , then the length of the chord of the larger circle which touches the smaller circle is-
Two chords AB and CD of a circle intersect at E such that AE = ., BE = . and CE = . The length of DE is -
In the given figure,
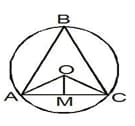
PQL and PRM are tangents to the circle with centre 'O' at the points Q and R, respectively and S is a point on the circle such that and . Then is equal to:
Find the length of the common chord of two circles of radii and , where the distance between their centres is