Motion in Two Dimensions

A football player is moving southward and suddenly turns eastward with the same speed to avoid an opponent. The force that acts on the player while turning is :

 If tangential acceleration vector of a speeding up particle at$P$is $3\hat{\mathrm{i}}+4\stackrel{⏜}{\mathrm{j}} \mathrm{m} {\mathrm{s}}^{-2}$ find the angle $\theta$
 

A particle attached to a light wire of length is projected horizontally with a velocity of $\surd 5gl$. Calculate its net acceleration when wire becomes horizontal.
 

Displacement of a particle in periodic motion is expressed as $x\left(t\right)=20 \cos \omega t$. If the time period of particle motion is $4 \mathrm{s}$, then displacement of the particle in $1 \mathrm{s}$ will be

Displacement of a particle is given $\overrightarrow{r}=3t \hat{i}+6 \hat{j}$. Find its velocity vector.

The position vector of a particle is given by $\mathrm{r} = 2\mathrm{t}\hat{\mathrm{i}}-5{\mathrm{t}}^2\hat{\mathrm{j}}$. What is the angle between initial velocity and initial acceleration?

On an open ground, a boy follows a track that turns to his left by an angle of $72°$ after every $10 \mathrm{m}$. Starting from a given turn, the displacement of the boy at the fourth turn will be

A ring of radius $10\mathrm{cm}$ is initially at the coordinate plane such that it touches the positive sides of the $x$ and $y$ axes at $P$ and $Q$ respectively. The ring starts rolling at a speed of $1\mathrm{rev}/\min$ along the positive $x$-axis. The coordinates of the point $Q$ after $2$ minutes and $45$ seconds are

A particle moves in the $X-Y$ plane with a constant acceleration of $1.5 \mathrm{m} {\mathrm{s}}^{-2}$ in the direction making an angle of $37°$ with the $X$-axis. At $t=0$ the particle is at the origin and its velocity is $8.0 \mathrm{m} {\mathrm{s}}^{-1}$ along the $X$-axis. Find the velocity and the position of the particle at $t=4·0 \mathrm{s}$.

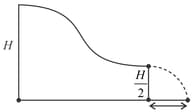
A small object slides down with initial velocity equal to zero from the top of a smooth hill of height $H$. The other end of the hill is horizontal and is at height $\frac{H}{2}$ as shown in the figure. The horizontal distance covered by the object from the end of the hill to the ground is

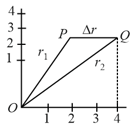
A particle is moving on a circular path of radius $r$ with uniform, speed $v$. What is the displacement of the particle after it has described an angle of $60°$?

A particle moves in a straight line so that distance $s=\sqrt{t}$ where $t$ is time, then the acceleration is proportional to

Three particles $A,B$ and $C$ are situated at the vertices of an equilateral triangle. They start moving with equal speeds (remains constant during the whole motion) such that $A$ always heads towards $B,B$ towards $C$ & $C$ towards  $A$. Finally they meet at a point. Find out the angle by which the line connecting $A$ and $B$ rotates with respect to initial orientation in space by the time distance between $A$ and $B$ reduces to half of the initial distance between $A$ and $B$.

Calculate displacement vector for a particle moving from point $P$ to $Q$.

A helicopter flies from a city $A$ to $B$. The line joining $A$ and $B$ is along north-south and its length is $100\mathrm{km}$. The speed of the helicopter is kept $100\mathrm{kmph}$ and wind blows from west to east with a speed of $60\mathrm{kmph}$. The time taken by the helicopter is

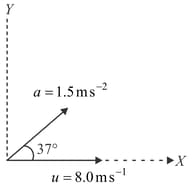
A particle moves along a path $ABCD$ as shown in the figure. Then the magnitude of net displacement of the particle from position $A$ to $D$ is:

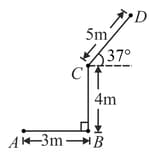
A particle $A$ is moving towards North and acceleration of $5 \mathrm{m} {\mathrm{s}}^{-2}$ and particle $B$ is moving North-East direction with an acceleration of $5\sqrt{2}\mathrm{m} {\mathrm{s}}^{-2}$. Find relative acceleration of particle $A$ with respect to particle $B$.

A wheel of radius $14\mathrm{cm}$ is rolling on a horizontal surface then find out the displacement of point of contact after the wheel completes $\frac{3}{4}$ Revolution.