Mathematical Formulation of a Linear Programming Problem

The corner points of the feasible region of a linear programming problem are $\left(0, 4\right), \left(8, 0\right)$, and $\left(\frac{20}{3},\frac{4}{3}\right)$. If $Z=30x+24y$ is the objective function, then (maximum value of $Z$ $-$ minimum value of $Z$) is equal to

Frame the below optimisation problem as a linear programming problem and determine its feasible region graphically.

Bhavani Singh, a farmer, decides to raise hens and cows to make some extra money apart from his agricultural income. He wants to raise no more than $16$animals including no more than $10$ hens. On an average it will cost him $\mathrm{Rs} 25$ and $\mathrm{Rs} 75$ per day to raise one hen and one cow respectively. He will make an average profit of $\mathrm{Rs} 12$ from each hen and $\mathrm{Rs} 40$ from each cow every day. He has a budget of $\mathrm{Rs} 900$ per day to raise the animals. How many of each type of animals should he raise to maximise his profit?

The constraints of a linear programming problem along with their graphs is shown below: 

$x + 2y \ge 3, x \ge 10, y \ge 0$

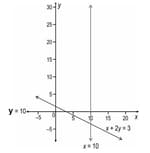
Which of the following objective functions has an optimal solution with respect to the above set of constraints? 

Solve the following problem by $LPP$

$Z_{max}=7x_1+5x_2$ such that

$-x_1-2x_2⩾-6,$

$4x_1+3x_2⩽12,$

$x_1,x_2⩾0$

A dietician wishes to mix two types of foods in such a way that vitamin contents of the mixture contain atleast $8$ units of vitamin A and $10$ units of vitamin $C$. Food $\text{'}I\text{'}$ contains $2$ units/kg of vitamin A and $1$ unit/kg of vitamin $C$. Food $\text{'}II\text{'}$ contains $1$ unit/kg of vitamin A and $2$ units/kg of vitamin $C$. It costs $\mathrm{Rs} 50$ per $\mathrm{kg}$ to purchase Food $\text{'}I\text{'}$ and $\mathrm{Rs} 70$ per kg to purchase Food $\text{'}II\text{'}$. Formulate this problem as a linear programming problem to minimise the cost of such a mixture.

Minimise $Z=3x+2y$ subject to the constraints:

$x+y\ge 8 ...\left(1\right)$

$3x+5y\le 15 ...\left(2\right)$

$x\ge 0, y\ge 0 ...\left(3\right)$ 

Determine graphically the minimum value of the objective function

$Z=-50x+20y ...\left(1\right)$

subject to the constraints:

$2x-y\ge -5 ...\left(2\right)$

$3x+y\ge 3 ...\left(3\right)$

$2x-3y\le 12 ...\left(4\right)$

$x\ge 0, y\ge 0 ...\left(5\right)$

Solve the following problem graphically:

Minimise and Maximise $Z=3x+9y ...\left(1\right)$

subject to the constraints: $x+3y\le 60 ...\left(2\right)$

$x+y\ge 10 ...\left(3\right)$

$x\le y ...\left(4\right)$

$x\ge 0, y\ge 0 ...\left(5\right)$

Solve the following linear programming problem graphically:

Minimise $\mathrm{Z}=200x+500y ...\left(1\right)$

subject to the constraints:

$x+2y\ge 10 ...\left(2\right)$

$3x+4y\le 24 ...\left(3\right)$

$x\ge 0, y\ge 0 ...\left(4\right)$

Solve the following linear programming problem graphically: 

Maximise $Z=4x+y ...\left(1\right)$

subject to the constraints:

$x+y\le 50 ...\left(2\right)$

$3x+y\le 90 ...\left(3\right)$

$x\ge 0, y\ge 0 ...\left(4\right)$

A company produces two types of goods, $A$ and $B$, that require gold and silver. Each unit of type $A$ requires $3 \mathrm{g}$ of silver and $1 \mathrm{g}$ of gold, while that of type $B$ requires $1 \mathrm{g}$ of silver and $2 \mathrm{g}$ of gold. The company can use at the most $9 \mathrm{g}$ of silver and $8 \mathrm{g}$ of gold. If each unit of type $A$ brings a profit of $₹ 40$  and that of type $B$ $₹ 50$, find the number of units of each type that the company should produce to maximize the profit. Formulate and solve graphically the LPP and find the maximum profit.

The feasible region for an LPP is always a _____ polygon.

A small firm manufactures necklace and bracelets. The total number of necklace and bracelet that it can handle per day is at most $24$. It takes $1$hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is $16$. If the profit on a necklace is $₹100$ and that on a bracelet is $₹300$, how many of each should be produced daily to maximize the profit? It is being given that at least one of each must be produced.

Mr.Dass wants to invest $₹12000$ in public provident fund ($\mathrm{PPF}$) and in national bonds. He has to invest at least $₹1000$ in $\mathrm{PPF}$ and at least $₹2000$ in bonds. If the rate of interest on $\mathrm{PPF}$ is $12\%$ per annum and that on bonds is $15\%$ per annum, how should he invest the money to earn maximum annual income? Also find the maximum annual income.

For the following Linear Programming problems with given constraints $4x+6y\le 60, 2x+y\le 20 \text{and} x\ge 0, y\ge 0$. The maximum value of $z=2x+3y$ is

For the following linear Programming problems, subject to the constraints $x+y\le 4$ and $x\ge 0$ , $y\ge 0$. Find the maximum value of $Z=3x+4y$

For the following linear Programming problem, subject to the constraints $x+2y\le 8$, $3x+2y\le 12$ and $x\ge 0$ , $y\ge 0$. Find the minimum value of $Z=-3x+4y$.

Maximize $z=x+2y$ subject to $x+2y\ge 50$, $2x-y\le 0$, $2x+y\le 100$, $x, y>0$.

Prizes are to be distributed among the students of class $XI$ and class $XII$. It is decided that at least $5$ students from class $XI$ and at least $4$ students from class $XII$ should get the prizes.The prize amount for class $XI$ students is $Rs 300$ and that for the class $XII$ students is $Rs 400$. The total number of prize holders should not be less than $10$ and more than $15$. How many students from each standard be selected to maximise the amount of prize money?

Prizes are to be distributed among the students of class $XI$ and class $XII$. It is decided that at least $5$ students from class $XI$ and at least $4$ students from class $XII$ should get the prizes.The prize amount for class $XI$ students is $Rs 300$ and that for the class $XII$ students is $Rs 400$. The total number of prize holders should not be less than $10$ and more than $15$. How many students from each standard be selected to minimise the amount of prize money?