Chords of a Circle
Chords of a Circle: Overview
This Topic covers sub-topics such as Alternate Segment Theorem and Angle Subtended in Same Segment
Important Questions on Chords of a Circle
In the given figure, is a cyclic quadrilateral, is tangent to the circle at point and is its diameter. If and find .
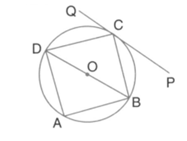
In the given figure, is the diameter. The tangent at meets produced at If find .
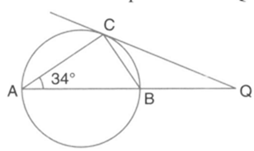
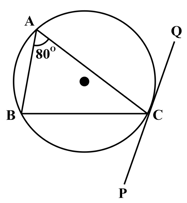
In the given figure, is the tangent at point and is a straight line. If and find .
In the given figure, is the tangent at point and is a straight line. If and find .
If is a tangent to the circle at calculate Given that, is the centre of the circle and angle
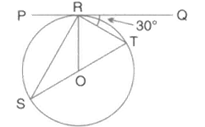
In the following figure, is the tangent to the circle at is the diameter and is the centre of the circle. If and calculate
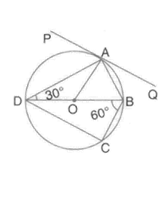
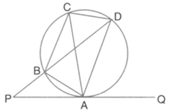
According to figure answer the following questions:
(i) is an alternate segment of circle.
(ii) is an alternate segment of circle.
(iii) If is joined with then is equal to which angle?
(iv) and is equal to which angle?
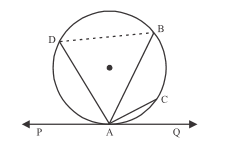
In the given figure, is tangent to the circle with centre , at point on its circumference and is parallel to Chord . If is a line segment, show that
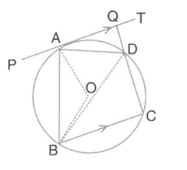
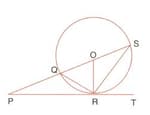
In the given circle with centre with centre and is a tagent to the circle at Find and
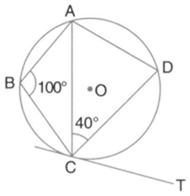
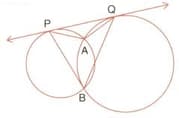
Two circles intersect each other at points and Their common tangent touches the circles at points and as shown in the figure. Show that the angles and are supplementary.
Two circles touch each other internally at a point A chord of the bigger circle intersects the other circle in and Prove that
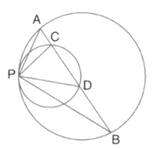
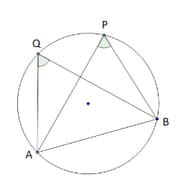
Two circles with centres and are drawn to intersect each other at points and Centre of one circle lies on the circumference of the other circle and is drawn tangent as to the circle with centre at Prove that bisects angle
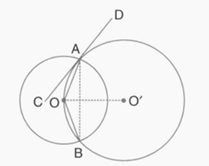
In the given figure, touches the circle with centre at point . Diameter is produced to meet the tangent at . Given and write an expression connecting and
In the given figure, touches the circle with centre at point . Diameter is produced to meet the tangent at . Given and prove that
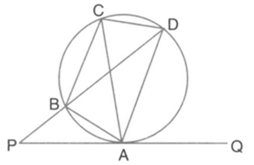
In the figure below, in a cyclic quadrilateral , diagonal bisects the angle . Then prove that diagonal is parallel to the tangent of a circle which passes through the points .
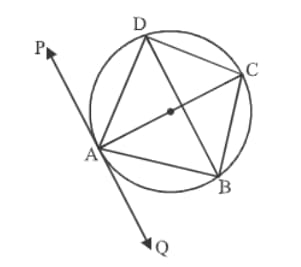
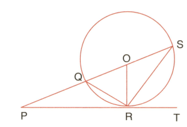
According to figure, and are parallel tangents. If then find the value of .
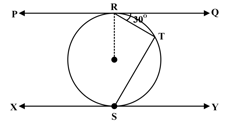
According to the figure, if then find the value of