Number of Tangents from a Point on a Circle

A circle with centre O is inscribed in a quadrilateral ABCD as shown in the figure. Which of the following statements is are true?

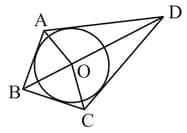
A. $\angle AOD+\angle BOC=180°$
B. $\angle \mathrm{AOB} \mathrm{and} \angle \mathrm{COD}$ are complementary.
C. $OA, OB, OC$ and $OD$are the angle bisectors of $\angle A, \angle B$ and $\angle C$ respectively.

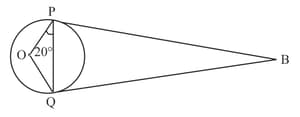
In the figure, $BP$ and $BQ$ are the tangents to the circle with centre $O$. If $\angle OPQ=20°$, then the measure of $\angle PBQ$ is

A circle is drawn. Two points are marked outside the circle such that only $3$ tangents can be drawn to the circle using these two points.

Which of the following is true based on the above information?

Shown below is a circle with $3$ tangents $KQ, KP$ and $LM$. $QL=2 \mathrm{cm}$ and $KL=6 \mathrm{cm}$.$PM=\frac{1}{2} KL$

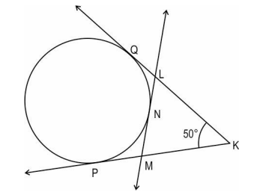
What is the measure of $\angle LMK$ ?

Prove that there is one and only one tangent at any point on the circumference of a circle.

In the given △ABC, AB = 12 cm, BC = 8 cm and AC = 10 cm. Find AD.

People of village want to construct a road nearest to a circular village Rampur. The road cannot pass through the village . But the people want the road should be at the shortest distance from the cente of the village.

Suppose , the road start from point $O$, which is outside the circular village and touch the boundary of the circular village at point A such that $OA=20 cm$ and also , the straight distance of the point $O$ from the centre $C$ of the village is $25 cm.$

Find the shortest distance of the road from the centre of the village.

If a point is inside the circle, how many tangents can be drawn from that point? Also, if two circles are externally and they do not touch, then find the number of common tangents.

In the given figure, $△ABC$ is circumscribed touching the circle at $P, Q$ and $R$ if $AP=4 \mathrm{cm}$, $BP=6 \mathrm{cm}$, $AC=12 \mathrm{cm}$ then find the radius of the circle.

Prove that the point $(1, - 1)$ lies within the circle $x^2 + y^2 - 4x + 6y + 4 = 0.$

Find the position of the point $\left(2,3\right)$  with respect to the circle $x^2+y^2-6x-4y=0$.

Find the position of the point $\left(3,4\right)$  with respect to the circle $x^2+y^2=9$

Find the position of the point $\left(5,12\right)$  with respect to the circle $x^2+y^2=169.$

In the given figure, $\mathrm{O}$ is the centre of the circle and $\mathrm{AB}=15 \mathrm{cm}$ and $\mathrm{AC}=7.5 \mathrm{cm}$. If the radius of the circle is $r \mathrm{cm}$, then find the value of $r$.

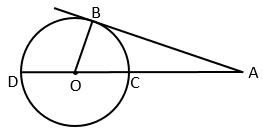
The radius of a circle is $8 \mathrm{cm}$. If the length of a tangent drawn to this circle from a point at a distance of $10 \mathrm{cm}$ from its centre is $k \mathrm{cm}$, then find the value of $k$.

In the given figure, tangent $\mathrm{PT}=12.5 \mathrm{cm}$ and $\mathrm{PA}=10 \mathrm{cm},$ find $\mathrm{AB}.$

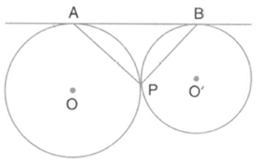
In the given figure, two circles touch each other externally at point $\mathrm{P}$. $\mathrm{AB}$ is the direct common tangent of these circle prove that tangent at point $\mathrm{P}$ bisect $\mathrm{AB}$.

In the figure, if $\mathrm{AB}=\mathrm{AC}$ then prove that $\mathrm{BQ}=\mathrm{CQ}$. 

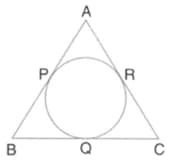
From the given figure, prove that $\mathrm{AP}+\mathrm{BQ}+\mathrm{CR}=\mathrm{BP}+\mathrm{CQ}+\mathrm{AR}.$ Also, show that $\mathrm{AP}+ \mathrm{BQ} +\mathrm{CR} =\frac{1}{2}\times \text{perimeter of}△\mathrm{ABC}$.

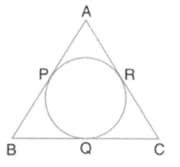
If the sides of a parallelogram touch a circle, prove that the parallelogram is a rhombus. 

Two circle touch each other internally. Show that the tangent drawn to the two circle from any point on the common tangent, are equal in length.