Congruence of Triangles
Congruence of Triangles: Overview
This topic covers concepts, such as, Congruent Figures, Congruence of Two Circles, Congruence of Two Squares, Congruence of Two Triangles, Notation for Congruence of Two Triangles & Corresponding Parts of Congruent Triangles etc.
Important Questions on Congruence of Triangles
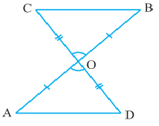
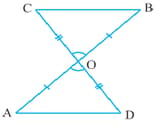
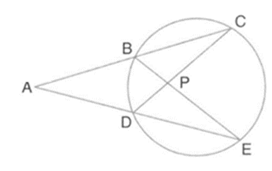
In figure, and intersect at .
Find and
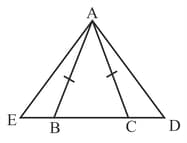
In the adjoining figure, is an isosceles triangle with and also given that . Prove that .
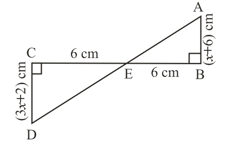
Use the congruency of triangles to find the value of and in following figure.
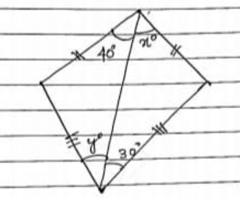
Use the congruency of triangles to find the value of and in following figure.
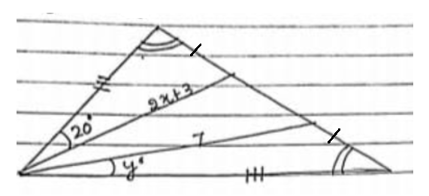
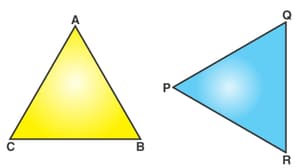
Given that , so explain what it means and if side units, then find the length of side .
Given that , so explain what it means and if side units, then find the length of side .
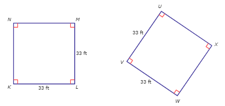
Which of the following figures are congruent to the square .
Define the congruency of two triangles.
How can two squares have the same angles but not be congruent?
Two squares are congruent if both of them have the same length of the _____.
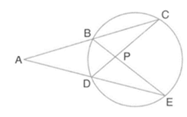
In the figure below, O is the centre of the circle. A and B are points on the circle. ∠OAP and ∠OBP are right angles.

Which of the following congruence rules can we use to prove PA = PB?
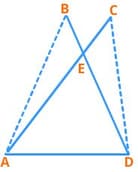
In the figure below, AE = DE and BE = CE.
Choose the suitable approach to prove that AB = CD.
From a point outside a circle, with circle , tangent and are drawn. Prove that .
Show that the circle drawn with any one of the equal sides of an isosceles triangle as diameter bisects the base of that isosceles triangle.