Criteria for Congruence of Triangles
Criteria for Congruence of Triangles: Overview
This Topic covers sub-topics such as AAS Congruence Rule, SSS Congruence Rule, ASA Congruence Rule, Criteria for Congruence of Triangles, RHS Congruence Triangle and, SAS Congruence Rules
Important Questions on Criteria for Congruence of Triangles
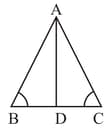
In triangle and is the midpoint of , show that .
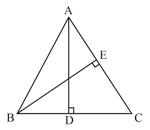
is an equilateral triangle, are perpendiculars to respectively. Prove that,
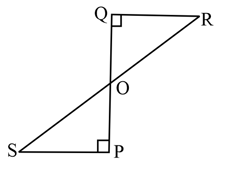
In the given figure, and are equal perpendiculars to . The length of is always equal to the length of
Explain ASA congruency
Three angles of one triangle are respectively equal to the three angles of the other. Further any one side of the two triangles being equal is sufficient to prove the two triangles congruent.
"Two triangles with a pair of equal angles are congruent."
Why is it necessary to have the side between the two angles be of the same length for both the triangles?
Rita says, 'For two triangles to be congruent, any three parameters of the six ( sides and angles) should be equal.'
Give examples in favour of and against her statement.
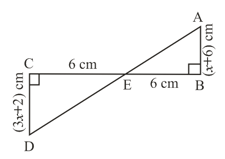
In the given figure, . Prove that
In the given figure, is the angle bisector of and . Prove that is an isosceles triangle.
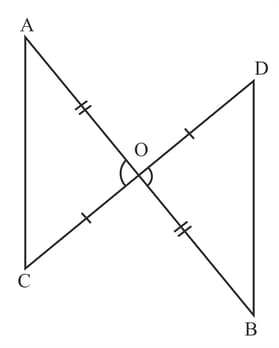
In figure, and intersect at .
Prove that
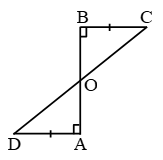
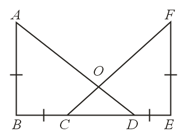
In the figure below, O is the mid-point of AB and CD, prove that .
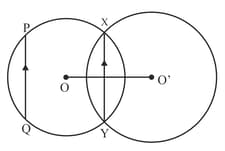
In the given figure, two circles with centres intersects at . is a chord of one circle parallel to (as shown in the figures). Prove that produced bisects .
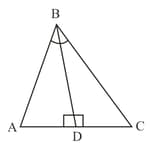
In the given figure, is an isosceles triangle with . Also is the angular bisector of .
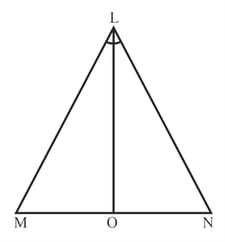
Use the ASA criterion to prove that . Also show that is the mid-point of .
is a tangent at to a circle whose center is , , where is a chord through , the end point of the diameter . Prove that is tangent at .
In the figure, is ? If yes, write the condition of congruence.
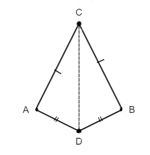
If line segment bisect each other at then using side angle side congruence rule prove that .
are two isosceles triangles. Show that is the perpendicular bisector of side .
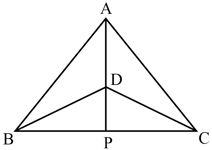
In and . Bisector of meets at . Prove .
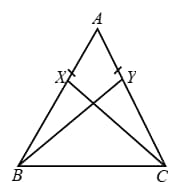
In Fig. X and Y are two points on equal sides and of a such that . Prove that .
and are equal perpendiculars to a line segment . Then _____ . [bisects/trisects]