Similarity of Triangles

In the given figure, $AD= 2 \mathrm{cm}, DB= 3 \mathrm{cm}, DE= 2.5 \mathrm{cm} \text{and} DE\parallel BC$. The value of $x$ is:

If $\mathrm{}\mathrm{A}\mathrm{D}$ and $\mathrm{}\mathrm{P}\mathrm{M}$ are medians of triangles $\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}$ and $\mathrm{}\mathrm{P}\mathrm{Q}\mathrm{R}$, respectively where $\mathrm{}∆\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{}~\mathrm{}∆\mathrm{}\mathrm{P}\mathrm{Q}\mathrm{R}$, prove that $\frac{\mathrm{A}\mathrm{B}}{\mathrm{P}\mathrm{Q}}=\frac{\mathrm{A}\mathrm{D}}{\mathrm{P}\mathrm{M}}$

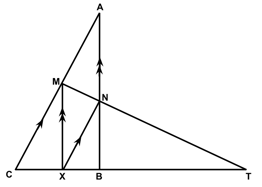
$X$ is a point on side $BC$ of $∆ABC$. $XM$ and $XN$ are drawn parallel to $AB$ and $AC$ respectively meeting $AB$ in $N$ and $AC$ in $M$. If $MN$ produced meets $CB$ at $T$ then

Prove that: $T{X}^2=TB\times TC$

In the given figure, $XZ$is parallel to $BC$. $AZ = 3 cm, ZC = 2 cm, BM = 3 cm$ and $MC = 5 cm$. Find the length of $XY$.

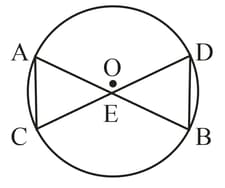
If the given figure $AB$and $CD$are two chords of a circle intersecting at $E$. Prove that $△EAC~ △EDB$ and hence show that $EA\times EB=EC\times ED$.

$△ABC~△JKL$ such that $AP$and $JQ$are angle bisectors of $△ABC$ and $△JKL$ respectively. If $AP: JQ=2:3$, then $\left(\frac{AB+AP}{JK+JQ}\right)+\left(\frac{BC+AC}{KL+JL}\right)$ is

If triangle $∆PQR$ similar to triangle $∆ABC$ and $PQ=6 \mathrm{cm}$,  $AB=8 \mathrm{cm}$ and the perimeter of a triangle $∆ABC$ is $36 \mathrm{cm}$, then perimeter of triangle $∆PQR$ is

In $∆LMN$ $\mathrm{seg} LM\cong \mathrm{seg} LN$.  $Seg. MP$ & $Seg. MQ$ are constructed from point $M$, which makes congruent angle along with $MN$. It intersects extended $LN$ at point $P$ & $Q$ respectively.

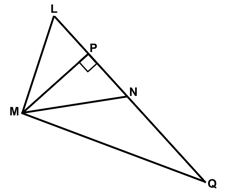
Prove that $\frac{L{M}^2}{L{Q}^2}=\frac{LP}{LQ}$

Shown below is a sector of a circle with centre $\mathrm{P}$. All lengths are measured in $\mathrm{cm}$.

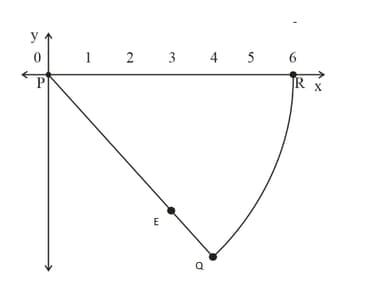
What is the length of $\mathrm{PE}$?

Choose and write the correct option in the following question.

In the figure given below, $PQ\parallel CB$

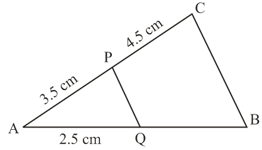
To the nearest tenth, what is the length of $QB$?

$ABCD$is a trapezium with $AB\parallel DC$, the diagonals $AC$and $BD$are intersecting at $E$. If $△AED$ iş similar to $△BEC$ then prove that $AD=BC$.

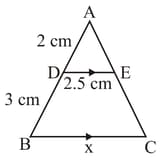
In the adjoining figure, if $EF\parallel DC\parallel AB$, find the value of $x$

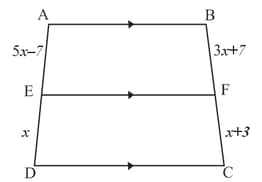
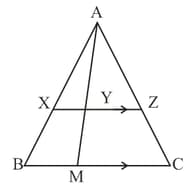
$P$ is any point on side $BC$ of a $∆ABC$. $PM\parallel BA$ and $PN\parallel CA$. $MN$ produced meets $CB$ produced at $Q$. Prove that $Q{P}^2=QB\times QC$.

$\mathit{∆}ABC$ and $\mathit{∆}PQR$ are similar triangles. $A_{\mathit{1}}$ and $A_{\mathit{2}}$ are the areas, $P_{\mathit{1}}$ and $P_{\mathit{2}}$ are the perimeters of $\mathit{∆}ABC$ and $\mathit{∆}PQR$ respectively.

Which of these is same as the ratio of the height of $\mathit{∆}ABC$ to that of $\mathit{∆}PQR$?

1. $\frac{A_1}{A_2}$
2. $\frac{P_1}{P_2}$
3. $\sqrt{\frac{A_1}{A_2}}$
4. $\sqrt{\frac{P_1}{P_2}}$

$∆ABC~∆PQR$; if $AB= 4 \mathrm{cm}, PQ= 6 \mathrm{cm} \text{and} QR= 9 \mathrm{cm}$, then $BC=$?

Shown below is a sector of a circle with centre $\mathrm{P}$. All lengths are measured in $\mathrm{cm}$.

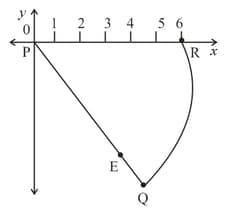
What is the length of $\mathrm{PE}$?

Assertion $\left(\mathrm{A}\right)$: If ratio of perimeters of two similar triangles is $6:11$, then ratio of their corresponding medians is also $6:11$.

Reason $\left(\mathrm{R}\right)$: Converse of B.P.T. states that if two sides of a triangle are divided by a line in equal ratio then the line is parallel to the third side.

In the figure, $\angle BED=\angle BDE$ & $\mathrm{E}$ divides $BC$ in the ratio $2:1$. Prove that $\mathrm{AF}\times \mathrm{BE}=2\mathrm{AD}\times \mathrm{CF}$.

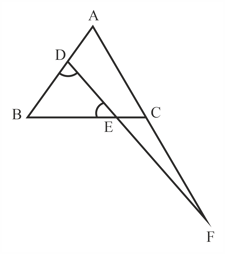
In the adjoining figure, find $\mathrm{QR}$, if $\mathrm{ST}\parallel \mathrm{QR}$.

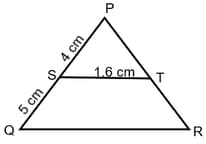
In a triangle ABC, the side AB is bisected at the point D and the line segment CD is bisected at the point E. If AE produced intersects BC at the point. F, then prove that$FC=\frac{1}{3}BC$.