Magnetic Field on the Axis of a Circular Current Loop

Find out the expression for the magnetic field at a point on the centre of a coil of radius carrying current I and having N number of turns.

A current carrying wire AB of the length $2\mathrm{\pi R}$ along a circle, as shown in figure. The magnetic field at the centre O is

A wire of length$0.20 \mathrm{m}$  is bent in the form of circular loop. If  $2 \mathrm{A}$ of current is flowing through this loop calculate the magnetic field at the centre of the loop and at a point P which is at a distance $15 \mathrm{cm}$ from the centre on its axis.

A current passing through a circular coil of two turns produces a magnetic field $B$ as its centre. The coil is then rewound so as to have four turns and the same current is passed through it. The magnetic field at its centre now is

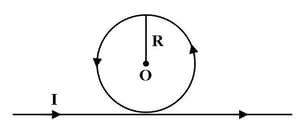
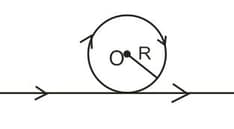
An infinitely long straight conductor is bent into the shape as shown below. It carries a current of $I$ ampere and the radius of the circular loop is $R$ metre. Then, the magnitude of magnetic induction at the centre of the circular loop is -

A current loop consists of two identical semicircular parts each of radius $R$, one lying in the x-y plane and the other in x-z plane. If the current in the loop is $i$, The resultant magnetic field due to the two semicircular parts at their common centre is

A straight conductor of length $l$ carrying a current $I,$ is bent in the form of a semicircle. The magnetic field (in tesla) at the centre of the semicircle is

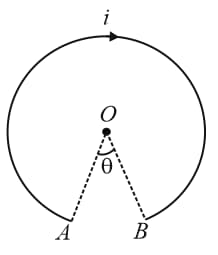
A cell is connected between the points $A$ and $C$ of a circular conductor $ABCD$ with $O$ as centre and angle $AOC=60°$. If $B_1$ and $B_2$ are the magnitudes of the magnetic fields at $O$ due to the currents in $ABC$ and $ADC$ respectively, then ratio $\frac{B_1}{B_2}$ is

Two circular current coils are concentric and their planes are mutually perpendicular and the magnetic field due to each coil is $B$, as shown in the figure: the net magnetic field at their common center will be

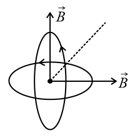
Two circular coils $\mathrm{X}$ and $\mathrm{}\mathrm{Y}$, having equal number of turns and carrying current in the same sense. Subtend same solid angle at point $\mathrm{O}$ if the smaller coil $\mathrm{X}$ is midway between $\mathrm{O}$ and coil $\mathrm{Y}$. ${\mathrm{B}}_{\mathrm{y}}$ is magnetic fied due to coil $\mathrm{Y}$ and that due to smaller coil $\mathrm{X}$ at $\mathrm{O}$ is ${\mathrm{B}}_{\mathrm{x}},$ then find the ratio $\frac{{\mathrm{B}}_{\mathrm{x}}}{{\mathrm{B}}_{\mathrm{y}}}$

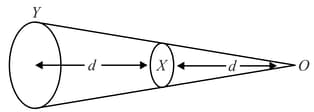
A very long conducting wire is bent in a semi-circular shape from A to B as shown in figure. The magnetic field at point P for steady current  configuration is given by

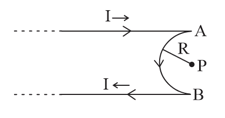
Magnetic field at point O will be

A circular loop of radius 5cm carries an electric current. Let P and Q be two points on the axis of the loop at distance 1 m and 2 m respectively from the center. If the magnetic field at P due to the current is 16mT, that at Q will be about

A current passing through a circular coil of two turns produces a magnetic field $B$ at its centre. The coil is then rewound so as to have four turns and the same current is passed through it. The magnetic field at its centre now is

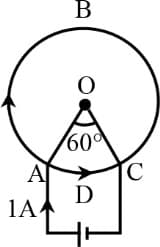
A current $\mathrm{I}$ is flowing through the loop, as shown in the figure. The magnetic field at centre $\mathrm{O}$ is 

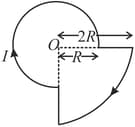
A long wire carries a steady current. It is bent into a circle of one turn and the magnetic field at the centre of the coil is $B.$ It is then bent into a circular loop of $n$ turns. The magnetic field at the centre of the coil will be

Charge $q$ is uniformly distributed on a thin ring of radius $R.$ The ring rotates about its axis with a uniform frequency $f \mathrm{Hz}$ . The magnitude of magnetic induction at the centre of the ring is

Two concentric coils of 10 turns each are placed in the same plane. Their radii are 20 cm and 40 cm and carry 0.2 A and 0.3 A current respectively in opposite directions. The magnetic field (in tesla) at the centre is

A long wire carries a steady current. It is bent into a circle of one turn and the magnetic field at the centre of the coil is $B$. It is then bent into a circular loop of $n$ turns. The magnetic field at the centre of the coil will be,