Motion in a Horizontal Circular Track

The time period of a conical pendulum is $T$. The tension in the string is, in the usual notation,

A particle describes a horizontal circle with uniform speed on the smooth surface of an inverted cone. The height of the horizontal plane above the vertex of the cone is $10 \mathrm{m}$. What is the speed of the particle if $g=10 \mathrm{m} {\mathrm{s}}^{-2}$?

A pendulum consisting of mass less string of length $20 \mathrm{cm}$ and a bob of mass $100 \mathrm{g}$ is set up as conical pendulum. Its bob now performs $75 \mathrm{rpm}$. Calculate the KE and increase in gravitational P.E. $\left(\text{Take}, {\pi }^2=10\right)$

While taking turn on a curved road, a cyclist has to bend through a certain angle. This is done

The time period of conical pendulum is given by

A conical pendulum of length $L$ makes an angle $\theta$ with the vertical as shown in the figure. The time period will be

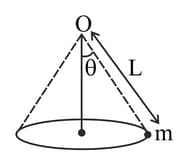
A string of length $L$ is fixed at one end and carries a mass $M$ at the other end. The string makes $2/\pi$  revolutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is:

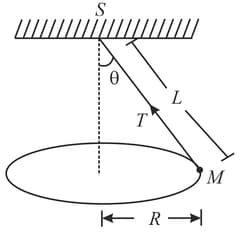
Why banking is necessary for circular road?

A car of mass $2000 \mathrm{kg}$ rounds a curve of radius $250 \mathrm{m}$ at $90 \mathrm{km}/\mathrm{hr}$. Calculate the frictional force required?

A spherical bob hangs from a light inextensible string and moves in a horizontal circle with string making angle $\theta$ with the vertical. The length $l$ of the string is then very slowly increased so that the motion is circular at all times to a good approximation. If $h$ is the height from center of the circle to the pivot and $r$ is the radius of the circle then $h\propto r^a$. The value of $a$ is

A car of mass $2000 \mathrm{Kg}$ is moving with a speed of 10 $\mathrm{m}{\mathrm{s}}^{-1}$on a circular path of radius $20 \mathrm{m}$ on a level road. What must be the frictional force between the car and the road so that the car does not slip?

The minimum velocity (in $\mathrm{m}{\mathrm{s}}^{-1}$) with which a car driver must traverse a flat curve of radius 150 m and coefficient of friction 0.6 to avoid skidding is

A string of length $L$ is fixed at one end and carries a mass $M$ at the other end. The string makes $\frac{2}{\pi }$ revolutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is :-

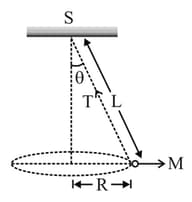
A disc revolves with a speed of $120$ $\mathrm{rev}./\min .$ and has a radius of $15 \mathrm{cm}.$ Two coins $\mathrm{A}$ and $\mathrm{B}$ are placed at $4 \mathrm{cm}$ and $14 \mathrm{cm}$ away from the centre of the record. If the coefficient of friction between the coins and the record is $0.16.$ which of the coins will revolve with the record ?

If a conical pendulum of length $\ell$ makes an angle $\theta$ with the vertical then time period of rotation will be:

Study the statements given below and find which is/ are true?

I. When a bus suddenly stops, the passengers tend to fall forward.

II. When stone is rotated in a circle of smaller radius, greater force is required.

III. At optimum speed, the frictional force is not needed at all to provide the necessary centripetal force in case of a banked road.

A conical pendulum is moving in a circle with angular velocity $\omega$ as shown. If tension in the string is $T,$ which of following equation are correct ?

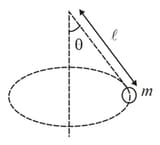
A string of length $0.5 \mathrm{m}$ carries a bob of mass $0.1 \mathrm{kg}$ with a period $\sqrt{2} \mathrm{s}$. Calculate angle of inclination of string with vertical and tension in the string.

A cyclist moves in a circular track of radius $100m$. If the coefficient of friction is $0.2$, then the maximum speed with which the cyclist can take a turn without leaning inwards, is-