Kepler's Laws

Satellites $A \text{and }B$ are orbiting around the earth in orbits of ratio $R \text{and} 4R$, respectively. The ratio of their areal velocities is

If a new planet is discovered rotating around the sun with the orbital radius double that of earth, then what will be its time period approximated to the nearest integer (in earth's days)?

(Take $\sqrt{2}=1.414$)

What does areal velocity of a planet indicates?

If earth suddenly shrinks by one third of its present radius, the acceleration due to gravity will be.

The time period of an earth-satellite in circular orbit is independent of 

Derive an expression of the binding energy of a satellite at rest on the surface of the earth.

The binding energy of satellites at rest on the surface of the earth is numerically equal to its _____ energy.

The total energy of a satellite is negative. What does it indicate?

The binding energy of a satellite at rest on the surface of the earth is given as:

If a graph is plotted between ${\mathrm{T}}^2$ and ${\mathrm{r}}^3$ for a planet, then its slope will be (where, ${\mathrm{M}}_{\mathrm{S}}$ is the mass of the sun):

Assertion: The law of areas can be understood as a consequence of conservation of angular momentum.

Reason: The gravitational force is a conservative force.

Assertion:  Areal speed of planets moving around the sun remains constant.

Reason:  Gravitational force between planet and sun provides required centripetal force to the planet for revolution around the sun.

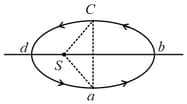
The figure shows elliptical path $abcd$ of a planet around the sun $S$ such that the area of triangle $CSA$ is $\frac{1}{4}$ the area of the ellipse. (see figure) with $DB$ as the major axis, and $CA$ as the minor axis. If ${\mathrm{t}}_1$ is the time taken for the planet to go over path $ABC$ and ${\mathrm{t}}_2$ for path taken over $CDA$ then:

Two satellites of masses $\mathrm{M}$ and $9\mathrm{M}$ are orbiting a planet in a circular orbit of radius $\mathrm{r}$. Their frequency of revolution will be in the ratio of

A planet moving around the sun sweeps area $A_1$ in $5$ days, $A_2$ in $10$ days and $A_3$ in $12$ days, then find the relation between $A_1$, $A_2$ and $A_3$.

According to Kepler's second law of planetary motion, the areal velocity of a planet revolving around the sun

State Kepler's second law of planetary motion.

What do you understand by the areal velocity of a planet?

Assume that the earth moves around the sun in a circular orbit of radius $R$ and there exists a planet which also move around the sun in a circular orbit with an angular speed twice as large as that of the earth. The radius of the orbit of the planet is

Kepler discovered