Bernoulli’s Theorem and Its Applications

Calculate the rate of flow of glycerine of density $1.25\times {10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$ through the conical section of a pipe if the radii of its ends are $0.1 \mathrm{m} \& 0.04 \mathrm{m}$ and the pressure drop across its length is $10 \mathrm{N} {\mathrm{m}}^{-2}$

How does Newton's third law apply ping pong?

What law of motion is ping pong?

Are ping pong balls pressurized?

How does the floating ping-pong ball work?

What is the force of a ping-pong ball?

Describe the motion of a ball without spin .

A ball moving without spinning in air than particles of air becomes stationary after large distance why?

Motion of ball without spin in air follow the path

If pressure on the ball at the top be ${\mathrm{P}}_{\mathrm{T}}$ and bottom be ${\mathrm{P}}_{\mathrm{B}}$ then for ball moving without spin 

How a ball without spin in air?

Potential energy term of Bernoulli's equation is not considered for its application in:

The potential energy term in Bernoulli's equation is present due to:

Bernoulli's theorem is a restatement of :

The pressure of water in a pipe when tap is closed is $5.5\times {10}^5 \mathrm{N}·{\mathrm{m}}^{-2}.$ When the tap is opened, water pressure reduces to $5\times {10}^5 \mathrm{N}·{\mathrm{m}}^{-2}.$ The velocity with which the water comes out when tap is opened is $\underline{ }$ (Density of water is $1000 \mathrm{kg}{ \mathrm{m}}^{-3}$ )

Bernoulli's theorem is a consequence of

A cylindrical tank is filled with water to a level of $3 \mathrm{m}.$ A hole is opened at a height of $52.5 \mathrm{cm}$ from the bottom. The ratio of the area of the hole to that of the cross-sectional area of the tank is $0.1.$ The square of the speed with which water will be coming out from the orifice is _______
$\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

Calculate the velocity of efflux of water when a completely filled cylinder of height $20 \mathrm{m}$ is punched with a hole on the side wall near its bottom. (Take, $g=10\mathrm{ }\mathrm{m}\mathrm{ }{\mathrm{s}}^{-2}$.)

A fluid flows through a horizontal pipe having two different cross-sections of area $A$ and $2A$. If the pressure at the thin cross-section is $p$ and fluid velocity is $v$, the velocity and pressure at the thicker cross-section is (take the density of fluid as $\rho$)

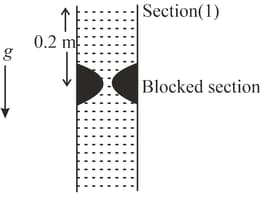
The normal inner cross-section area of an artery (section $\left(1\right)$) is $A$, the velocity of blood flow and the blood pressure (Gauge pressure) at that section are respectively $1 \mathrm{m} {\mathrm{s}}^{-1}$ and $1.2\times {10}^4 \mathrm{Pa}$. There is some blockage in the artery $0.2 \mathrm{m}$ vertically below the section $\left(1\right)$. When the blood pressure (Gauge) inside the blocked artery becomes less than or equal to the Gauge pressure outside the artery (that is ${10}^4 \mathrm{Pa}$) the artery gets collapsed and the person gets a heart attack. If the limiting area of cross-section of blood flow at the blocked section for heart-attack is $\frac{A}{n}$ then the value of $n$ will be..... (${\rho }_{\mathrm{blood}}={10}^3 \mathrm{kg} {\mathrm{m}}^{-3}, \mathrm{g}=10 \mathrm{m} {\mathrm{s}}^{-2}$, assume the blood as an ideal fluid)