Angular Momentum

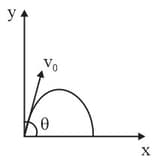
An object of mass $2 \mathrm{kg}$ is projected from ground, with initial velocity $40 \mathrm{m} {\mathrm{s}}^{-1}$, making angle $60°$ with the horizontal. Find its angular momentum about the point of projection when the object is at its maximum height. (Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)

State and prove principle of conservation of angular momentum. Explain it with examples.
 

Define angular momentum of a body. Obtain an expression for angular momentum of a rigid body rotating with uniform angular velocity. State its SI unit and dimensions.

A homogeneous rod $XY$of length $L$ and mass  '$M$' is pivoted at the centre '$C$ such that it can rotate freely in vertical plane. Initially the rod is in the horizontal position. A blob of wax of same mass '$M$' as that of the rod falls vertically with the speed '$V$and sticks to the rod midway between points $C$ and $Y$. If the rod rotates with angular speed '$\omega$' what will be angular speed in terms of $V$ and $L$ ?

A uniform circular disc with its plane horizontal is rotating about a vertical axis passing through its centre at a speed of $180$ r.p.m. A small piece of wax of mass. $1.9$ g falls vertically on the disc and sticks to it at a distance of $25$ cm from the axis. If the speed of rotation is now reduced by $60$ r.p.m., calculate moment of inertia of the disc.

Two wheels of moment of inertia $4 kg m^2$ rotate side by side at the rate of  $120$ rev/min and $240$ rev/min respectively in the opposite directions. If now both the wheels are coupled by means of weightless shaft so that both the wheels now rotate with a common angular speed, find the new speed of rotation

A flywheel in the form of disc is rotating about an axis passing through its centre and perpendicular to its plane loses $100J$ of energy, when slowing down from $60$ r.p.m. to $30$ r.p.m. Find its moment of inertia about the same axis and change in its angular momentum.

A ballet dancer spins about a vertical axis at $90$ rpm with arms outstretched. With the arms folded, the moment of inertia about the same axis of rotation changes to $75\raisebox{1ex}{$0$}\!\left/ \!\raisebox{-1ex}{$0$}\right.$. Calculate the new speed of rotation .

A small particle of mass $m$ is projected at an angle $\theta$ with the axis with an initial velocity $v_0$ in the x-y plane as shown in the figure. At a time $t<\frac{v_0\sin \theta }{g}$, the angular momentum of the particle is 

Which physical quantity is represented by the product of linear momentum and distance?

The moment of momentum is called

Which of the following physical quantity is represented by the product of the moment of inertia and angular velocity? 

Name the quantity represented by $\overrightarrow{r}\times \overrightarrow{p}$ ?

For s-orbital, orbital angular momentum is zero.

The angular momentum of a moving electron is an integral multiple of $\mathrm{h}/2\mathrm{\pi }$.

$\mathrm{h}/\mathrm{\pi }$ is the angular momentum in the _____ shell of helium. 

(Choose from: first/second/third/fourth)

A man stand on a rotating platform with his arms stretched is holding a $5 \mathrm{kg}$ weight in each hand. The angular speed of the platform is $1.2 \mathrm{rev} {\mathrm{s}}^{-1}$. The moment of inertia of the man together with the platform may be taken to be constant and equal to $6 \mathrm{kg} {\mathrm{m}}^2$. If the man brings his arms close to his chest with the distance of each weight from the axis changing from $100 \mathrm{cm}$ to $20 \mathrm{cm}$, the new angular speed of the platform is

Two bodies have moments of inertia $I$ and $2I$ respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio of

A solid cylinder of mass $20 \mathrm{k}\mathrm{g}$ and radius $20 \mathrm{c}\mathrm{m}$ rotates about its axis with an angular speed $100 \mathrm{rad} {\mathrm{s}}^{-1}$. The angular momentum of the cylinder about its axis is

The position of a particle is given by $\overrightarrow{r}=\widehat{\mathrm{i}}+2\widehat{\mathrm{j}}-\widehat{\mathrm{k}}$, and its linear momentum is given by $\overrightarrow{P}=3\widehat{\mathrm{i}}+4\widehat{\mathrm{j}}-2\widehat{\mathrm{k}}$. Then its angular momentum about the origin is perpendicular to