The Scalar Product of Vectors

 The projection of the vector $\overrightarrow{AB}$ on the directed line $l$, if angle $\theta =\pi$ will be

If $\overrightarrow{A}=(2\hat{i}+3\hat{j}-\hat{k}) \mathrm{m}$ and $\overrightarrow{B}=(\hat{i}+2\hat{j}+2\hat{k}) \mathrm{m}$. The magnitude of component of vector $\overrightarrow{A}$ along vector $\overrightarrow{B }$will be _____$\mathrm{m}$

Which of the following vector is perpendicular to the vector $\overrightarrow{A}=2\hat{i}+3\hat{j}+4\hat{k}$ ?

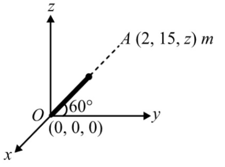
The $x-y$ plane is the horizontal ground and $z-$axis is vertical. A gun is placed at the origin and aimed at a point having coordinates $\left(2, 15, z\right) \mathrm{m}$. The gun makes an angle of $60°$ with $y$ direction. Height of the point $A$ above the ground is

If $\hat{\mathrm{a}}$ and $\hat{\mathrm{b}}$ are two unit vectors such that $\hat{\mathrm{a}}+2\hat{\mathrm{b}}$ and $5\hat{\mathrm{a}}-4\hat{\mathrm{b}}$ are perpendicular to each other, then the angle between $\hat{\mathrm{a}}$ and $\hat{\mathrm{b}}$ is:
Given $\left(5\hat{\mathrm{a}}-4\hat{\mathrm{b}}\right)·\left(\hat{\mathrm{a}}+2\hat{\mathrm{b}}\right)=0$

The two vectors $\overrightarrow{A}=2\hat{\mathrm{i}}+\hat{\mathrm{j}}+3\hat{\mathrm{k}}$ and $\overrightarrow{B}=7\hat{\mathrm{i}}-5\hat{\mathrm{j}}-3\hat{\mathrm{k}}$ are

Vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ lie in a $xy$ plane. $\overrightarrow{A}$ has magnitude $8.00$ and angle $130°$ with the $x$-axis $;\overrightarrow{B}$ has components $B_X=-7.72$ and $B_y=-9.20$. What are the angles between the negative direction of the $y$-axis and (a) the direction of $\overrightarrow{A}$ (b)  the direction of the product $\overrightarrow{A}\times \overrightarrow{B}$, and (c) the dirction of $\overrightarrow{A}\times \left(\overrightarrow{B}+3.00\hat{k}\right)$?

An ant starts from the origin and crawls $10 \mathrm{cm}$ along the $x$-axis and then $20 \mathrm{cm}$ along the $y$-axis. The dot product of the ant's displacement vector with the position vector of a point that makes $45°$ with the $x$-axis and has a magnitude of $\sqrt{2} \mathrm{cm}$ is

A vector is given as $\overrightarrow{A}=4\hat{\mathrm{i}}+7\hat{\mathrm{j}}$. What would be the angle, the vector $\overrightarrow{A}$ makes with $y$-axis

If vectors are $\overrightarrow{A}=\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}$ and $\overrightarrow{B}=-\hat{\mathrm{i}}-\hat{\mathrm{j}}-\hat{\mathrm{k}}$, then find the angle between $\left(\overrightarrow{A}-\overrightarrow{B}\right)$ and $\overrightarrow{A}$.

The particles $A$ and $B$ move in $x-y$ plane such that both have constant acceleration ${\overrightarrow{a}}_{\mathrm{A}}=-10\hat{j} \mathrm{m} {\mathrm{s}}^{-2}$ and ${\overrightarrow{a}}_B=-5\hat{j} \mathrm{m} {\mathrm{s}}^{-2}$ respectively. The velocities of particles at $t=0$ are ${\overrightarrow{\mathrm{u}}}_{\mathrm{A}}=-5\hat{i}+20\hat{j} \mathrm{m} {\mathrm{s}}^{-1}$ and ${\overrightarrow{u}}_B=-2.5\hat{i}+10\hat{j} \mathrm{m} {\mathrm{s}}^{-1}$. At time $t=0$, particle $A$ is at origin and particle $B$ is at point having coordinates ($5$ metres,$0$). Find the instant of time in seconds at which angle between velocity of $A$ and velocity of $B$ is $180°$

The angle between two vectors $\overrightarrow{A}=2\hat{i}+\hat{j}-\hat{k}$ and $\overrightarrow{B}=\hat{i}-2\hat{j}-3\hat{k}$ is

Vectors $\overrightarrow{p}$ and $\overrightarrow{q}$ are such that$|\overrightarrow{p}·\overrightarrow{q}|=|\overrightarrow{p}\times \overrightarrow{q}|$ , what is magnitude of $r=\overrightarrow{p}+\overrightarrow{q}$.

The angle between $A\text{ and }B\text{ is }\theta$. The value of the triple product $\overrightarrow{A}·\overrightarrow{B}\times \overrightarrow{A}$ isEnable GingerCannot connect to Ginger Check your internet connection
or reload the browserDisable in this text fieldRephraseRephrase current sentenceEdit in Ginger×

The position of a particle is $\overrightarrow{r}=\left(a \cos \omega t\right) \hat{\mathrm{i}}+\left(a \sin \omega t\right) \hat{\mathrm{j}}$. . The velocity vector of the particle is

Given that $\overrightarrow{a}·\overrightarrow{b}=0\text{ and }\overrightarrow{a}\times \overrightarrow{c}=0$. Then the angle between $\overrightarrow{b}\text{ and }\overrightarrow{c}$ is

The projection of $\overrightarrow{a}$ on $\overrightarrow{b}$ is

If $\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\times \overrightarrow{b}\right|$ then the angle between $\overrightarrow{a}\text{ and }\overrightarrow{b}$ is,

The vector sum of two forces is perpendicular to their vector difference. In that case, the forces are

If $\left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{a}-\overrightarrow{b}\right|$, the angle between $\overrightarrow{a}\text{ and }\overrightarrow{b}$ is