Distance and Displacement

The displacement $x$ of particle moving in one dimension, under the action of a constant force is related to the time $t$ by the equation $t=\sqrt{x}+3$ where $x$ is in meters and $t$ in seconds. Find the displacement of the particle when its velocity is zero.

A particle moves in a circle of radius $R.$ Find its displacement and the distance covered for half the period of its revolution.

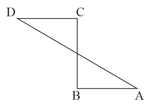
A boy moves from A to B through $5 \mathrm{cm}$, B to C through $12 \mathrm{cm}$ and again from C to D through $5 \mathrm{cm}$. Find his displacement.

A particle moving along the path $y=x^2$, from $x=0 \mathrm{m}$ to $x=2 \mathrm{m}$. Then the distance travelled by the particle is

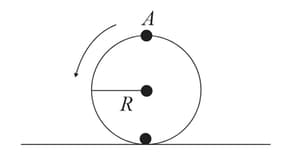
A disc is rolling without slipping on a surface. The radius of the disc is $R.$ At $t=0,$ the top most point on the disc is $A$ as shown in figure. When the disc completes half of its rotation, the displacement of point $A$ from its initial position is

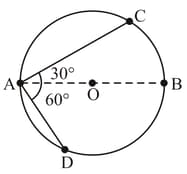
Two particles move from A to C and A to D on a circle of radius R and diameter AB. If the time taken by both particles are the same, then the ratio of magnitudes of their average velocities is

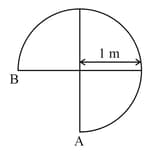
In one second, a particle goes from point A to B moving in along circle shown in figure. The magnitude of its average velocity is

If position of a particle is $x= 5t^2-20t+2$, find distance and displacement at $t= 4 \mathrm{s}$.

A body is moving along the circumference of a circle of radius R and completes half of the revolution. Then, the ratio of the displacement to distance is 

An insect can crawl on the floor. If it starts crawling from one corner of a cubical room of slde '$a$' Minimum distance it would crawl to raech the furthermost corner in the room.

A frog takes $5$ leaps in forward direction and $2$ leaps backward. A pot hole is $22 \mathrm{cm}$ a head of the frog. If the distance covered in $1$ leap is $1 \mathrm{cm}$. Find the distance travelled by frog before it falls in the pothole.

An aeroplane is flying from city $A$ to city $B$ along path $1$ . The path $1$ is a circular arc whose centre coincides with the centre of the Earth. Another aeroplane is flying along path $2$ from $A$ to $B$. The path $2$ is circular arc whose centre is at $C.O$ is the centre of the Earth. Then,

​​​​​​​

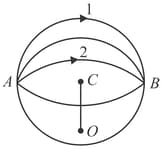
A person runs along a circular path of radius $5 \mathrm{m}$. If he completes half of the circle find the magnitude of the displacement vector. How far the person ran?

Let ${\mathrm{x}}_1$ and ${\mathrm{x}}_2$ be the positions of an object at time ${\mathrm{t}}_1$ and ${\mathrm{t}}_2$. Then, its displacement, denoted by A, in time $\mathrm{\Delta t} =\mathrm{B}$, is given by the difference between the C and D position.
Here A,B,C and D refer to 

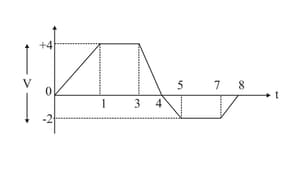
The velocity-time graph of a particle in linear motion is shown. Both $v$ and $t$ are in SI units. What is the displacement of the particle from the origin after $8$ second.

When a car moves towards east $50 \mathrm{m}$ then towards south $50 \mathrm{m}$, later on towards west $50 \mathrm{m}$, finally towards north $50 \mathrm{m}$, the displacement of the car in magnitude is

The speed of particle moving along a straight line becomes half after every next second (in every on second speed is constant). The initial speed is $v_2$. The total distance travelled by the particle will be

A body starting at a point, say A, reaches, say B, ahead in a straight line and returns back to A. Find its net displacement.

In a desert, a beetle 's motion sends fast longitudinal pulses, $v_L=150{ \mathrm{ms}}^{-1}$ and slower transverse pulses. $v_{\mathrm{s}}=50{ \mathrm{ms}}^{-1}$, along the sand's surface. The sand scorpion has eight legs: spread roughly in a circle of $5\mathrm{cm}$ diameter, intercepts the faster longitudinal pulses $4.0 \mathrm{ms}$ earlier than the slower transverse pulse. The pray is located at a distance of:

The displacement $x$ of a particle moving in one dimension under the action of a constant force is related to time $t$ by the equation $t=\sqrt{x}+3$, where $x$ is in meters and $t$ is in seconds. What is the displacement of the particle from $t=0 \mathrm{s}$ to $t=6 \mathrm{s}$?