Pythagoras Theorem
Pythagoras Theorem: Overview
In this topic, we will prove the Pythagoras theorem using the concept of similarity of triangles. We will also learn new theorems that are used to solve problems.
Important Questions on Pythagoras Theorem
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
The sides of a triangle are given below. Determine whether it is a right triangle. In case of a right triangle, write the length of its hypotenuse.
.
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
In Fig. is a point in the interior of a triangle and . Show that
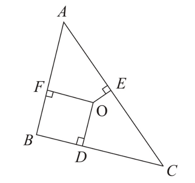
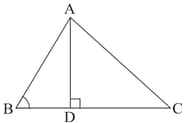
In Fig. is a triangle right-angled at and . Show that

In the figure, is a triangle right-angled at and . Show that
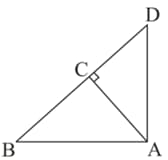
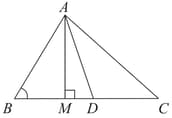
In the given figure, is a median of a triangle and . Prove that
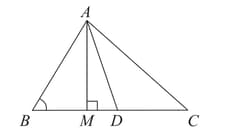
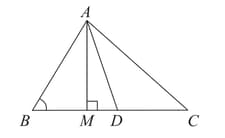
In the figure, is the median of triangle and . Prove that:
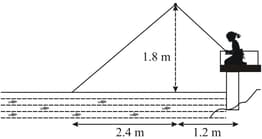
Nazima is fly fishing in a stream. The tip of her fishing rod is above the surface of the water and the fly at the end of the string rests on the water away and from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see the given figure)? If she pulls in the string at the rate of per second, what will be the horizontal distance of the fly from her after seconds?
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
In the figure, is a median of a triangle and . Prove that :
In the figure given below is a triangle in which and . Prove that .
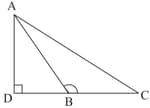
is a triangle in which and produced. Prove that
In and . The angle is
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
In an equilateral triangle is a point on side such that . Prove that .
The perpendicular from on side of a intersects at such that . Prove that
and are points on the sides and respectively of a triangle right-angled at . Prove that .
Two poles of heights and stand on a plane ground. If the distance between the feet of the poles is , find the distance between their tops.
An aeroplane leaves an airport and flies due north at a speed of . At the same time, another aeroplane leaves the same airport and flies due west at a speed of . How far apart will be the two planes after ?
