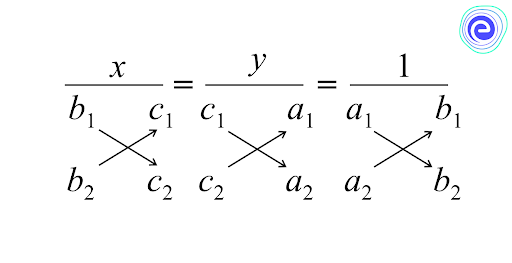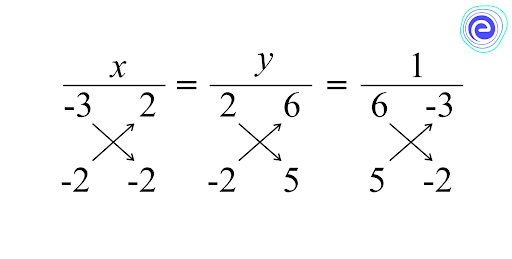Algebraically Solving Simultaneous Linear Equations: Definition, Types, and Examples

The equation in the form of \(ax+b=0\) or \(ax=b,\) where \(a\) and \(b\) are real numbers and \(a≠0\) is called a linear equation in one variable \(x.\) Similarly, an equation of form \(ax+by+c=0\) or \(ax+by=c\) is called a linear equation in two variables. A solution or a root of the equation is a value of the variable that makes \({\rm{LHS}} = {\rm{RHS}}\) and therefore satisfies the equation when substituted in the equation.

In this article, we will study the meaning of linear equations, simultaneous linear equations, and the methods for Algebraically Solving Simultaneous Linear Equations along with examples.

Linear Equations in Two Variables

The general form of linear equations in two variables is \(ax+by+c=0\) or \(ax+by=c,\) where \(a, b, c\) are real numbers, \(a, b≠0\) and \(x, y\) are variables.

Example: \(3x+2y=4, -6x+5y=4\) are linear equations in two variables.

Any pair of values of \(x\) and \(y\) which satisfies the equation \(ax+by+c=0\) or \(ax+by=c\) is called its solution.

Simultaneous Linear Equations in Two Variables

A pair of linear equations in two variables is said to form a system of simultaneous linear equations.

Below are few examples of the system of two simultaneous linear equations in two variables:

(i) \(3x+2y=2\)

\(5x-y=4\)

(ii) \(7a+b-1=0\)

\(9a+8b-2=0\)

The general form of a pair of linear equations in two variables \(x\) and \(y\) is 

\(a_{1} x+b_{1} y+c_{1}=0\) and 

\(a_{2} x+b_{2} y+c_{2}=0\).

Solution

A solution is a pair of values of the variables \(x\) and \(y\) satisfying each of the equations in a given system of two simultaneous linear equations in \(x\) and \(y\).

Consistent System

If a system of simultaneous linear equations has at least one solution, it is consistent.

Inconsistent System

If a system of simultaneous linear equations has no solutions, it is inconsistent.

The given system of simultaneous linear equations can be solved using one of two methods. The graphical method is one, and the algebraic method is another.

Algebraically Solving Simultaneous Linear Equations

The graphical method is inconvenient most of the time, especially when the point of intersection of the lines represented by two provided equations has rational integers coordinates. The graphical method does not provide an accurate solution in many cases. For example, if the solution to a system of two linear equations is \(x=-\frac{4}{5}, y=\frac{5}{7}\) then by graphical method, the point of intersection would be \(\left(-\frac{4}{5}, \frac{5}{7}\right) .\)

This point is close to \((-0.8, 0.7)\) on graph paper, so it is not convenient to distinguish these two points; and while reading the coordinates of the point of intersection, we are likely to make an error. To get an accurate answer, you’ll need to apply a precise procedure. The following algebraic procedures are used to determine the correct answer.

Below are the methods to solve the simultaneous linear equations using algebraic methods:

1. Substitution method of solving the linear equations in two variables
2. Elimination method of solving the linear equations in two variables
3. Cross multiplication method of solving the linear equations in two variables
4. Solving the linear equations in two variables by comparison
5. Solving equations with interchangeable coefficients

Let us study each of the methods in detail.

Substitution Method of Solving the Linear Equations in Two Variables

In this method, we express one of the variables as the other variable from either of the two equations. Then, this expression is put in the other equation to obtain an equation in one variable, as explained in the following steps.

(i) Obtain the two equations. Let the equations be: 

\({a_1}x + {b_1}y + {c_1} = 0\) and \(\ldots \ldots (i)\)

\(a_{2} x+b_{2} y+c_{2}=0 \ldots \ldots . (ii)\)

(ii) Choose either of the two equations, say (i), and find the value of one variable, say \(y,\) in terms of the other, i.e. \(x.\)

\(y=\frac{-c_{1}-a_{1} x}{b_{1}}\)

(iii) Substitute the value of \(y,\) obtained in the previous step in equation (ii) to get an equation in \(x.\)

So, equation (ii) becomes,

\(a_{2} x+b_{2} \times \frac{-c_{1}-a_{1} x}{b_{1}}+c_{2}=0\)

(iv) Solve the equation obtained in the above step to get the value of \(x.\)

(v) Substitute the value of \(x\) so obtained in the expression for \(y\) obtained in the second step to get the value of \(y.\)

(vi) The values of \(x\) and \(y\) obtained in the fourth and fifth steps respectively constitute the solution of the given system of two linear equations.

Elimination Method of Solving the Linear Equations in Two Variables

This method eliminates one of the two variables to obtain an equation in one variable, which can easily be solved. Putting the value of this variable in any one of the given equations, the value of the other variable can be obtained. Let us follow the below steps to know about the elimination method:

1. Obtain the two equations.
2. Multiply the equations so that the variable coefficients are all the same.
3. Add or subtract the equations obtained in the second step as the terms having the same coefficients are of opposite or of the same sign.
4. Solve equations in one variable obtained in the third step.
5. Substitute the value obtained in the fourth step in any one of the given equations and find the value of the other variable. The values of the variables in the fourth and fifth steps constitute the solution of the given system of equations.

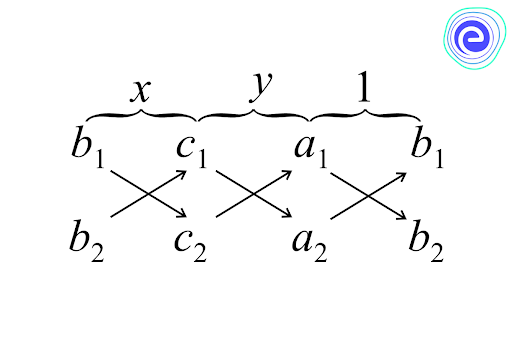
Cross Multiplication of Solving the Linear Equations in Two Variables

The below steps help us apply the cross-multiplication method directly.

The given system is, 

\(a_{1} x+b_{1} y+c_{1}=0\)

\(a_{2} x+b_{2} y+c_{2}=0\)

Step 1:

Write the coefficient as follows:

The arrows between the two numbers indicate that they are to be multiplied. The products with upward arrows are to be subtracted from the products with downward arrows.

Step 2:

The products are written as below:

i.e \(\frac{x}{b_{1} c_{2}-b_{2} c_{1}}=\frac{y}{c_{1} a_{2}-c_{2} a_{1}}=\frac{1}{a_{1} b_{2}-a_{2} b_{1}}\)

Step 3:

Taking \(\frac{x}{b_{1} c_{2}-b_{2} c_{1}}=\frac{1}{a_{1} b_{2}-a_{2} b_{1}}\), we get:

\(x=\frac{\left(b_{1} c_{2}-b_{2} c_{1}\right)}{\left(a_{1} b_{2}-a_{2} b_{1}\right)}\) and taking, 

\(\frac{y}{c_{1} a_{2}-c_{2} a_{1}}=\frac{1}{a_{1} b_{2}-a_{2} b_{1}}\) we get,

\(y=\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\)

Solving Equations with Interchangeable Coefficients

These are equations in which the coefficients of the two variables are interchanged around. As illustrated in the examples below, an easy method is used to solve such problems.

Example:

Solve: \(5x+3y=47\) and \(3x+5y=57\)

Solution: \(5x+3y=47 …….(i)\)

\(3x+5y=57 …….(ii)\)

Adding (i) and (ii), we get, \(8x+8y=104\)

\(⇒x+y=13 ……(iii)\)

Subtracting (ii) from (i), we get \(2x-2y=-10\)

\(⇒x-y=-5 ……(iv)\)

Adding (iii) and (iv), we get,

\(2x=8⇒x=4 \)

Substituting \(x=4\) in (iii), we get,\( 4+y=13\)

\(⇒y=13-4=9 \)

Therefore, \(x=4\) and \(y=9\).

Solving the Linear Equations in Two Variables by Comparison

From each of the given equations, express the unknown quantity in terms of the other and equate the expressions thus obtained.

Below is an example of solving simultaneous linear equations by comparison.

Example: 

Solve: \(4x-3y=6\) and \(5x-2y=11\)

Solution: \(4x-3y=6 ……(i)\)

\(5x-2y=11 ……(ii)\)

From (i), we get \(x=\frac{6+3 y}{4} \ldots . . . (iii)\)

From (ii), we get \(x=\frac{11+2 y}{5} \ldots \ldots (iv)\)

Equating (iii) and (iv), we get,

\(\frac{6+3 y}{4}=\frac{11+2 y}{5}\)

\(⇒30+15y=44+8y\)

\(⇒15y-8y=44-30\) 

\(⇒7y=14=2\) 

Substituting \(y=2\) in (iii), we get,

\(x=\frac{6+3(2)}{4}\)

\(⇒x=3\)

Therefore, \(x=3\) and \(y=2\).

Solved Examples – Algebraically Solving Simultaneous Linear Equations

Q.1. Solve \(9x+7y=71\) and \(4x-3y=1\).
Ans:
\(9x+7y=71 ……(i)\)
\(4x-3y=1 ……(ii)\)
From (i), we get \(y=\frac{71-9 x}{7} \ldots \ldots (iii)\)
From (ii), we get \(y=\frac{4 x-1}{3} \quad \ldots \ldots(iv)\)
Equating (iii) and (iv), we get,
\(\frac{71-9 x}{7}=\frac{4 x-1}{3}\)
\(\Rightarrow 3(71-9 x)=7(4 x-1)\)
\(\Rightarrow-27 x-28 x=-7-213\)
\(\Rightarrow-55 x=-220\)
\(\Rightarrow x=4\)
Substituting \(x=4\) in (iii), we get \(y=\frac{71-9(4)}{7}\)
\(\Rightarrow y=\frac{71-36}{7}=\frac{35}{7}\)
\(\Rightarrow y=5\)
Therefore, \(x=4\) and \(y=5\).

Q.2. Solve the given system of equations by the cross-multiplication method.
\(6x – 3y = \, – 2\) 
\(5x – 2y = 2\) 
Ans: Writing the given equations in general form, we get
\(6x-3y+2=0 ……(i)\)
\(5x-2y-2=0 ……(ii)\)
Using cross-multiplication, we get,

\(\Rightarrow \frac{x}{6-(-4)}=\frac{y}{100-(-12)}=\frac{1}{-12-(-15)}\)
\(\Rightarrow \frac{x}{10}=\frac{y}{22}=\frac{1}{3}\)
Taking \(\frac{x}{10}=\frac{1}{3} \Rightarrow 3 x=10 \Rightarrow x=\frac{10}{3}\)
Taking \(\frac{y}{22}=\frac{1}{3} \Rightarrow 3 y=22 \Rightarrow y=\frac{22}{3}\)
Therefore \(x=\frac{10}{3}\) and \(y=\frac{22}{3}\)

Q.3. Solve for x and y by the interchangeable method.
\(101x + 99y = 499\) 
\(99x + 101y = 501\) 
Ans:
\(101 x+99 y=499 \ldots \ldots . .(\mathrm{i})\)
\(99 x+101 y=501 \ldots \ldots(\mathrm{ii})\)
Adding (i) and (ii), we get,
\(200x+200y=1000\)
\(\Rightarrow x+y=5…… (iii)\)
Subtracting (ii) from (i), we get,
\(2 x-2 y=-2 \Rightarrow x-y=-1 \ldots \ldots (iv)\)
Adding (iii) and (iv), we get,
\(2x=4⇒x=2\) 
Substituting \(x=2\) in equation (iii), we get:
\(2+y=5⇒y=3\) 
Therefore, \(x=2\) and \(y=3\).

Q.4. Solve for x and y by substitution method:
\(3x + 2y = 0\) and \(2x + 5y = \, – 11\)
Ans:
\(3x+2y=0 ……(i)\)
\(2x+5y=-11 ……(ii)\)
From (i), we get \(y=\frac{-3 x}{2} \quad \ldots \ldots (iii)\)
Substituting (iii) in (ii), we get,
\(2 x+5\left(\frac{-3 x}{2}\right)=-11\)
\(\Rightarrow 2 x-\frac{15 x}{2}=-11\)
\(\Rightarrow \frac{-11 x}{2}=-11\)
\(\Rightarrow x=2\)
Substituting \(x=2\) in (iii), we get,
\(y=\frac{-6}{2}=-3\)
Therefore, \(x=2\) and \(y=-3\).

Q.5. Solve for x and y by the elimination method.
\(7x – 2y = 2\) and \(3x + 4y = 30\)
Ans:
\(7x-2y=2 ……(i)\)
\(3x+4y=30 ……(ii)\)
Multiplying equation (i) by \(2,\) we get,
\(14x-4y=4 ……(iii)\)
Adding (ii) and (iii), we get,
\(17x=34⇒x=2 \)
Substituting \(x=2\) in equation (ii), we get,
\(3(2)+4 y=30 \Rightarrow 4 y=24 \Rightarrow y=6\)
Therefore,\( x=2\) and \(y=6\)

Summary

In this article, we have learnt the meaning of simultaneous linear equations, different types to solve that simultaneous equation algebraically, and some example problems on algebraically solving simultaneous linear equations. A pair of values of the variables (x) and (y) satisfying each of the equations in a given system of two simultaneous linear equations in (x) and (y) is called a solution of the system. Some methods to solve the simultaneous linear equations using algebraic methods are given below:

1. Substitution method of solving the linear equations in two variables
2. Elimination method of solving the linear equations in two variables
3. Cross multiplication of solving the linear equations in two variables
4. Solving the linear equations in two variables by comparison
5. Solving equations with interchangeable coefficients.

FAQs on Algebraically Solving Simultaneous Linear Equations

The frequently asked questions on methods for algebraically solving simultaneous linear equations are answered here:

Q.1. What are simultaneous linear equations?
Ans: A pair of linear equations in two variables is said to form a system of simultaneous linear equations.
The general form of simultaneous linear equations are:
\(a_{1} x+b_{1} y+c_{1}=0\) and 
\(a_{2} x+b_{2} y+c_{2}=0\).

Q.2. Name the methods to solve the simultaneous linear equations algebraically.
Ans: Some methods to solve the simultaneous linear equations using algebraic methods are given below:
1. Substitution method of solving the linear equations in two variables
2. Elimination method of solving the linear equations in two variables
3. Cross multiplication of solving the linear equations in two variables
4. Solving the linear equations in two variables by comparison
5. Solving equations with interchangeable coefficients.

Q.3. How do you solve a pair of linear equations?
Ans: We can solve a pair of linear equations graphically and algebraically.

Q.4. What are solutions in simultaneous linear equations in two variables?
Ans: A pair of values of the variables \(x\) and \(y\) satisfying each of the equations in a given system of two simultaneous linear equations in \(x\) and \(y\) is called a solution of the system.

Q.5. When two linear equations are in two variables, what are they called?
Ans: When two linear equations are in two variables, they are called simultaneous linear equations.

Now that you have a detailed article on Algebraically solving simultaneous linear equations, we hope you study well. If you get stuck somewhere do let us know in the comments sections. We will get back to you at the earliest.