Definite Integration: Definite integrals are used to find the area of the curve in a graph. These have lower and upper limits. The limits can be taken as \([a, b]\) to find the area of the curve \(f(x)\) with respect to the \(x-\) axis. The definite integration can also be used to find the area of a circle, parabola, and ellipse i.e., it is mainly used to find the area under the curve, area between two curves and area bounded by a curve and a line. In this article, let us learn about definite integral and its properties.

What is Definite Integral?

A definite integral is an area under the curve between two fixed limits. It is represented as \(\int_{a}^{b} f(x) d x\)

where,

\(a\) is the lower limit

\(b\) is the upper limit

Sometimes \(a, b\) are called limits of integration, for a function \(f(x)\) defined with the reference to \(x-\) axis.

Area Under a Curve

To find the area under the curve between two limits, we divide the area into small rectangle strips and then sum their individual areas to find the area under the curve. The more the rectangles, the more accurate the area is, so we divide the area into infinite rectangles, each with the same size.

How To Solve Definite Integrals?

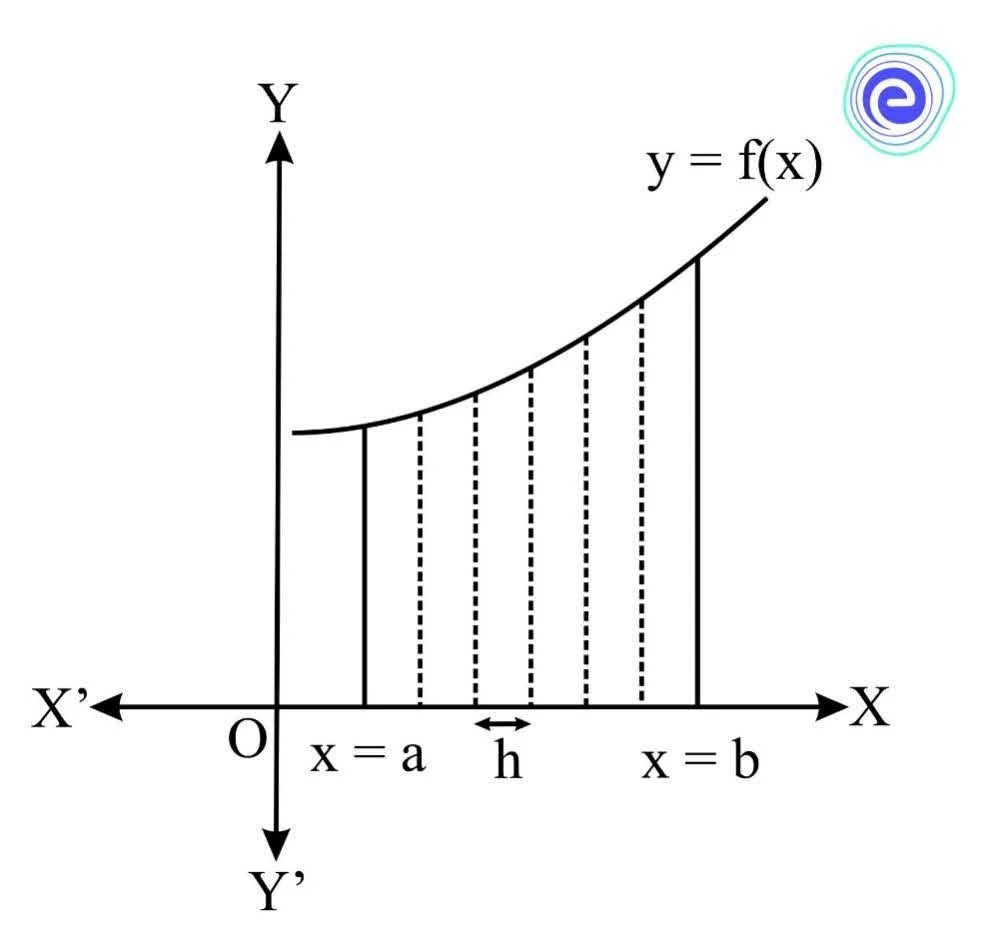
Definite integrals are solved using the fundamental theorem of calculus. It links the concept of integrating a function with its differentiation. The fundamental theorem of calculus validates the procedure by calculating the difference between the antiderivative at the upper and lower limits.

What is the Fundamental Theorem of Calculus?

Fundamental theorems of calculus are very useful as they are used to find definite integral or they will be helpful to find the area between the curves. There are two parts of the fundamental theorem of calculus.

Let us discuss the first and second fundamental theorem of calculus.

First Fundamental Theorem of Calculus

The first fundamental theorem of calculus finds the derivative of an integral. It also establishes the connection between derivative and integral. Using the first fundamental theorem of calculus, we can find the derivative of a definite integral without actually finding the definite integral.

Statement: If \(f(x)\) is a continuous function over a closed interval \([a, b]\) and differentiable in open interval \((a, b)\) and if \(F(x)\) is defined as

\(F(x)=\int_{a}^{x} f(t) d t\)

Then,

\(F^{\prime}(x)=f(x)\) over the interval \([a, b]\)

\(\Rightarrow \frac{d}{d x} \int_{a}^{x} f(t) d t=f(x)\)

Let us take one example and find the result using the first fundamental theorem of calculus.

Example : Evaluate \(\frac{d}{d x} \int_{2}^{x} \frac{3+t}{1+t^{3}}\) using the fundamental theorem of calculus.

Solution : We have the first fundamental theorem of calculus as \(\frac{d}{d x} \int_{a}^{x} f(t) d t=f(x)\)

so we can apply this theorem as the lower limit is given constant i.e. \(2\) and upper limit given as variable \(x\), the we get

\(\frac{d}{d x} \int_{2}^{x} \frac{3+t}{1+t^{3}}=\frac{3+x}{1+x^{3}}\)

Second Fundamental Theorem of Calculus

The second fundamental theorem of calculus says the value of a definite integral of a function is obtained by substituting the upper limit and lower limit in the antiderivative of the function. To calculate a definite integral of a function, we will divide the area under the graph of that function lying within the given interval into many rectangles. Then, we add the areas of all such rectangles. The second fundamental theorem of calculus helps us evaluate a definite integral without calculating the area under the curve.

Statement: The second fundamental theorem of calculus states that, if \(f(x)\) is continuous on the closed interval \([a, b]\) and \(F(x)\) is and antiderivative of \(f(x)\) on \([a, b]\), then \(\int_{a}^{b} f(x) d x=F(b)-F(a)\)

Example: Evaluate \(\int_{0}^{1} x d x\)

Solution: Let \(I=\int_{0}^{1} x d x\)

Now, we will first find integral using a standard formula. Then, we get \(\int x d x=\frac{x^{2}}{2}+C\)

Now, substitute the upper and lower limits in order, then

\(\left(\frac{1}{2}+C\right)-(0+C)=\frac{1}{2}\)

The integral constant \(C\) is always cancelled while applying limits. We neglect \(C\) while finding the definite integral.

Definite Integral as Limit of Sum

As explained earlier, the area under a curve between two given limits can be expressed as the sum of an infinite number of rectangles. To evaluate the definite integral \(\int_{a}^{b} f(x) d x\) using this concept, we divide the area under the curve into many rectangles by dividing \([a, b]\) into an infinite number of subintervals.

So, the definite integral as limit sum formula is given by,

\(\int_a^b f (x)dx = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{r = 1}^n h f(a + rh)\)

Where, \(h=\frac{b-a}{n}\) is the length of each subinterval.

Let us see an example of determining definite integral as a limit sum.

Example: Evaluate \(\int_{0}^{1} x d x\) using definite integral as a limit sum.

Solution: On comparing with \(\int_{a}^{b} f(x) d x\), we get \(f(x)=x, a=0 ; b=1\)

So, we have, \(h=\frac{b-a}{n}=\frac{1-0}{n}=\frac{1}{n}\)

Applying the above formula \(\int_a^b f (x)dx = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{r = 1}^n h f(a + rh)\), then we get

\(\int_0^1 x dx = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{r = 1}^n {\frac{1}{n}} f\left( {0 + \frac{r}{n}} \right)\)

\( = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{n = 1}^\infty  {\frac{1}{n}} \left( {\frac{r}{n}} \right)\)

\( = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^2}}}\sum\limits_{r = 1}^\infty  r \)

\( = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^2}}} \cdot \frac{{n(n + 1)}}{2}\)

\( = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^2}}}\frac{{{n^2}\left( {1 + \frac{1}{n}} \right)}}{2}\)

\(=\frac{(1+0)}{2}\)

\(\therefore \int_{0}^{1} x d x=\frac{1}{2}\)

Properties of Definite Integrals

The definite integral properties help us find the integral for a function multiplied by a constant, for the sum of the two or more functions, and even and odd functions.

Let us check the following properties of definite integrals, which are helpful to solve problems of definite integrals.

Property 1: \(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(t) d t\)

Proof : Substitute \(x=t\)

Now, differentiate with respect to \(x\), we get,

\(d x=d t\)

And also, when \(x=a\), then \(t=a\) and when \(x=b\), then \(t=b\)

Therefore, \(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(t) d t\)

Hence, proved.

Property 2: \(\int_{a}^{b} f(x) d x=-\int_{b}^{a} f(x) d x\)

In particular \(\int_{a}^{a} f(x) d x=0\)

Proof: Let \(F\) be the antiderivative of \(f\).

Then, by the second fundamental theorem of calculus, we have \(\int_{a}^{b} f(x) d x=F(b)-\)

\(F(a)=-[F(a)-F(b)]=-\int_{b}^{a} f(x) d x\)

Here, we observe that, if \(a=b\), then \(\int_{a}^{a} f(x) d x=0\)

Hence, proved.

Property 3: \(\int_{a}^{b} f(x) d x=\int_{a}^{c} f(x) d x+\int_{c}^{b} f(x) d x\) where \(a<c<b\)

Proof : Let \(F\) be the antiderative of \(f\).

Then, by the second fundamental theorem of calculus, we have

\(\int_{a}^{b} f(x) d x=F(b)-F(a) \ldots(i)\)

\(\int_{a}^{c} f(x) d x=F(c)-F(a) \ldots(i i)\)

\(\int_{c}^{b} f(x) d x=F(b)-F(c) \ldots(i i i)\)

Adding (ii) and (iii), then we get \(\int_{a}^{c} f(x) d x+\int_{c}^{b} f(x) d x=F(b)-F(a)=\int_{a}^{b} f(x) d x\)

Hence, proved.

Property 4 : \(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(a+b-x) d x\)

Proof: Substitute \(t=a+b-x\)

Now, differentiate with respect to \(x\). Then, we get,

\(-d x=d t\)

Also, when \(x=a\), then \(t=b\) and when \(x=b\), then \(t=a\)

Therefore.

\(\int_{a}^{b} f(x) d x=-\int_{b}^{a} f(a+b-t) d t\)

\(=\int_{a}^{b} f(a+b-t) d t\)

\(=\int_{a}^{b} f(a+b-x) d x\)

Hence, proved.

Property 5 : \(\int_{0}^{a} f(x) d x=\int_{0}^{a} f(a-x) d x\)

Proof: Substitute \(t=a-x\)

Now, differentiate with respect to \(x\),then we get,

\(-d x=d t\)

And also, when \(x=0\), then \(t=a\) and when \(x=a\), then \(t=0\)

Therefore,

\(\int_{0}^{a} f(a-x) d x=-\int_{a}^{0} f(t) d t\)

\(=\int_{0}^{a} f(t) d t\)

\(=\int_{0}^{a} f(x) d x\)

Hence, proved.

Property 6 : \(\int_{0}^{2 a} f(x) d x=\int_{0}^{a} f(x) d x+\int_{0}^{a} f(2 a-x) d x\)

Proof : Using property \(3\), we can write \(\int_{0}^{2 a} f(x) d x=\int_{0}^{a} f(x) d x+\int_{a}^{2 a} f(x) d x\)

Substitute \(t=2 a-x\) in the second integral on the right side

Now, differentiate with respect to \(x\), then we get,

\(dt = – dx\)

Thus, when \(x=a, t=a\) and when \(x=2 a, t=0\), Also \(x=2 a-t\)

Therefore, the second integral becomes \(\int_{a}^{2 a} f(x) d x=-\int^{0} f(2 a-t) d t=\)

\(\int_{0}^{a} f(2 a-t) d t=\int_{0}^{a} f(2 a-x) d x\)

Hence, \(\int_{0}^{2 a} f(x) d x=\int_{0}^{a} f(x) d x+\int_{0}^{a} f(2 a-x) d x\)

Property 7 :

(i) \(\int_{0}^{2 a} f(x) d x=2 \int_{0}^{a} f(x) d x\) if \(f(2 a-x)=f(x)\)

(ii) \(\int_{0}^{2 a} f(x) d x=0\) if \(f(2 a-x)=-f(x)\)

Proof: Using property \(6\), we have \(\int_{0}^{2 a} f(x) d x=\int_{0}^{a} f(x) d x+\int_{0}^{a} f(2 a-x) d x \ldots\) (1)

(i) Now, if \(f(2 a-x)=f(x)\), then \((1)\) becomes \(\int_0^{2a} f (x)dx = \int_0^a f (x)dx + \int_0^a f (x)dx = 2\int_0^a f (x)dx\)

(ii) Now, if \(f(2 a-x)=-f(x)\), then \((1)\) becomes \(\int_0^{2a} f (x)dx = \int_0^a f (x)dx – \int_0^a f (x)dx = 0\)

Hence, proved.

Property 8 :

(i) \(\int_{-a}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x\) if \(f(-x)=f(x)\) or \(f(x)\) is an even function.

(ii) \(\int_{-a}^{a} f(x) d x=0\) if \(f(-x)=-f(x)\) or \(f(x)\) is an odd function

Proof: Using property \(5\), we can write \(\int_{-a}^{a} f(x) d x=\int_{-a}^{0} f(x) d x+\int_{0}^{a} f(x) d x\)

Then substitute \(t=-x\) in the first integral on the right side

Differentiating with respect to \(x\), we get,

\(d t=-d x\)

Now, when \(x=-a, t=a\) and when \(x=0, t=0\)

Therefore, \(\int_{-a}^{a} f(x) d x=-\int_{a}^{0} f(-t) d t+\int_{0}^{a} f(x) d x\)

\(=\int_{0}^{a} f(-x) d x+\int_{0}^{a} f(x) d x \ldots\)….(1)

(i) Now, if \(f\) is an even function, then \(f(-x)=f(x)\), therefore, \((1)\) becomes

\(\int_{-a}^{a} f(x) d x=\int_{0}^{a} f(x) d x+\int_{0}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x\)

(ii) Now, if \(f\) is an odd function then \(f(-x)=-f(x)\), therefore,\((1)\) becomes

\(\int_{-a}^{a} f(x) d x=-\int_{0}^{a} f(x) d x+\int_{0}^{a} f(x) d x=0\)

Hence, proved.

Solved Examples – Definite Integration

Q.1. Find \(\int_{\frac{-\pi}{4}}^{\frac{\pi}{4}} \cos ^{2} x d x\)
Ans: Given: \(\int_{\frac{-\pi}{4}}^{\frac{\pi}{4}} \cos ^{2} x d x\)
\(\Rightarrow \int_{\frac{-\pi}{4}}^{\frac{\pi}{4}} \cos ^{2} x d x=2 \int_{0}^{\frac{\pi}{4}} \cos ^{2} x d x\) [Since \(\cos x\) is an even function, use the property \(\int_{-a}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x\), if \(f(-x)=f(x)\) ].
\(\Rightarrow \int_{\frac{-\pi}{4}}^{\frac{\pi}{4}} \cos ^{2} x d x=2 \int_{0}^{\frac{\pi}{4}} \frac{1+\cos 2 x}{2} d x\)
\(=\int_{0}^{\frac{\pi}{4}}(1+\cos 2 x) d x\)
\(=\left[x+\frac{\sin 2 x}{2}\right]_{0}^{\frac{\pi}{4}}\)
\(=\left(\frac{\pi}{4}+\frac{\sin \left(2 \times \frac{\pi}{4}\right)}{2}\right)-\left(0+\frac{\sin 0}{2}\right)\)
\(=\left(\frac{\pi}{4}+\frac{\sin \frac{\pi}{2}}{2}\right)-0\)
\(=\frac{\pi}{4}+\frac{1}{2}\)
\(\therefore \int_{\frac{-\pi}{4}}^{\frac{\pi}{4}} \cos ^{2} x d x=\frac{\pi}{4}+\frac{1}{2}\)

Q.2. Find the value of integral \(\int_{-1}^{3}\left(x^{2}+2\right) d x\) using the fundamental theorem of calculus.
Ans: Given: \(\int_{-1}^{3}\left(x^{2}+2\right) d x\)
Using the second fundamental theorem of calculus \(\int_{a}^{b} f(x) d x=F(b)-F(a)\), where \(F^{\prime}(x)=f(x)\)
Therefore, \(\int_{-1}^{3}\left(x^{2}+2\right) d x=\int_{-1}^{3}\left(x^{2}\right) d x+2 \int_{-1}^{3} d x\)
\(=\left[\frac{x^{3}}{3}+2 x\right]_{-1}^{3} \quad\left(\because \int x^{n} d x=\frac{x^{n+1}}{n+1}+C\right)\)
\(=\left[\frac{(3)^{3}}{3}+2(3)\right]-\left[\frac{(-1)^{3}}{3}+2(-1)\right]\) [Applying upper and lower limits]
\(=\left[\frac{27}{3}+6\right]-\left[\frac{-1}{3}-2\right]\)
\(=\frac{28}{3}+8\)
\(=\frac{28+24}{3}\)
\(\therefore \int_{-1}^{3}\left(x^{2}+2\right) d x=\frac{52}{3}\)

Q.3. Find the value of \(\int_{-4}^{4} x^{2} d x\)
Ans: Given: \(\int_{-4}^{4} x^{2} d x\)
Since \(x^{2}\) is an even function, so use the property,
\(\int_{-a}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x\), if \(f(-x)=f(x)\)
Therefore, \(\int_{-4}^{4} x^{2} d x=2 \int_{0}^{4} x^{2} d x\)
\(=2\left[\frac{x^{3}}{3}\right]_{0}^{4} \quad\left(\because \int x^{n} d x=\frac{x^{n+1}}{n+1}+C\right)\)
\(=2\left(\frac{4^{3}}{3}-0\right)\) [Applying upper and lower limits]
\(=2 \times \frac{64}{3}\)
\(\therefore \int_{-4}^{4} x^{2} \cdot d x=\frac{128}{3}\)

Q.4. Find the value of \(\int_{1}^{2} e^{x} d x\)
Ans:
Given: \(\int_{1}^{2} e^{x} d x\)
Using the second fundamental theorem of calculus \(\int_{a}^{b} f(x) d x=F(b)-F(a)\), where
\(F^{\prime}(x)=f(x)\)
Therefore, \(\int_{1}^{2} e^{x} d x=\left[e^{x}\right]_{1}^{2}\)
\(=e^{2}-e^{1}\) [Applying upper and lower limits]
\(=e^{2}-e\)
\(\therefore \int_{1}^{2} e^{x} d x=e(e-1)\)

Q.5. If \(\int_{0}^{3} f(x) d x=40\) and \(\int_{0}^{1} f(x) d x=-15\), then find the value of \(\int_{1}^{3} f(x) d x\)
Ans:
Given: \(\int_{0}^{3} f(x) d x=40\) and \(\int_{0}^{1} f(x) d x=-15\)
Using one of the properties of definite integrals,
\(\int_{a}^{b} f(x) d x=\int_{a}^{c} f(x) d x+\int_{c}^{b} f(x) d x\)
\(\therefore \int_{0}^{3} f(x) d x=\int_{0}^{1} f(x) d x+\int_{1}^{3} f(x) d x\)
\(\Rightarrow 40=-15+\int_{1}^{3} f(x) \cdot d x\)
\(\Rightarrow 40+15=\int_{1}^{3} f(x) \cdot d x\)
\(\therefore \int_{1}^{3} f(x) \cdot d x=55\)

Summary

The definite integral is the area under the curve between two fixed limits. It is represented as \(\int_{a}^{b} f(x) d x\) where \(a\) is the lower limit, and \(b\) is the upper limit. Using the first fundamental theorem, we can find the derivative of a definite integral without finding the definite integral. The second fundamental theorem of calculus says that the value of a definite integral of a function is obtained by substituting the upper and lower limits in the antiderivative of the function. Definite integrals can mainly be used to find the area under the curve and between two curves.

Frequently Asked Questions (FAQs)

Q1. What is definite integration?
Ans: The definite integral is expressed as \(\int_{a}^{b} f(x) \cdot d x\)
Where,
\(a\) is the lower limit.
\(b\) is the upper limit.
Definite integral is the antiderivative of the function \(f(x)\) to find the function \(F(x)\), So we can write
\(\int_{a}^{b} f(x) \cdot d x=[F(x)]_{a}^{b}=F(b)-F(a)\)

Q2. What is definite integration used for?
Ans: The definite integrals are used to find the area of the curves, such as circle, ellipse and parabola. The standard formulas of indefinite integrals can be used to find the area of irregular shapes. The area of the small space is determined by applying the upper and lower limits.

Q3. What is definite and indefinite integration?
Ans: The following points are generalised between definite and indefinite integral:

Definite Integral	Indefinite Integral
Definite integrals are defined within the limits.	Indefinite integrals do not have limits.
The final answer of the definite integral is unique.	In indefinite integrals, the final is mostly an expression.
The integration constant is not present.	The integration constant is always present in the final answer.

Q4. How do you solve definite integration?
Ans: To evaluate or solve the definite integral, we follow the simple steps given below:
Step 1: Find the indefinite integral using the standard formula of indefinite integration [without limits].
Step 2: Substitute the upper limit and lower limit, respectively.
Step 3: Finally, find the result by subtracting results obtained from step 2.

Q5. What is the definite integral of \(1\)?
Ans: The definite integral of \(1\) can be determined by using
\(\int_{a}^{b} f(x) d x=[F(x)]_{a}^{b}=F(b)-F(a)\)
\(\Rightarrow \int_{a}^{b} 1 d x=(x)_{a}^{b}=b-a\)
In simple words, we can say that the definite integral of \(1\) is the difference between the upper limit and the lower limit.

Q6. What is the difference between definite integral and area?
Ans: Finding the area under a region is the application of finding the integral value. Definite integrals can also be used to find the area under the curve, the area between two curves. If a function is strictly positive, then the area between the function and the \(x-\) axis is simply the required definite integral. If the function is simply negative, then the area is negative of the definite integral.

We hope you find all the information about the Definite Integration in this article. If you have any further queries, drop us a comment below. We will get back to you. Till then, stay tuned to Embibe for all updates on Definite Integration, exam preparation tips and the latest academic articles!