HCF and LCM: Full Form, and Examples

HCF and LCM: Students willing to know HCF and LCM formula can refer to this article. The LCM and HCF full forms are Lowest Common Multiple full and Highest Common Factor, respectively. These concepts occupy significance both in school-level mathematics as well as in higher classes. Basic Arithmetic plays a vital role when it comes to building a solid foundation in Mathematics. Mathematics is difficult and interesting at the same time.

If the concepts are clear right from the beginning, then students will find it interesting and also, they will not face challenges understanding the advanced concepts taught in the higher classes. Students must read this article to understand all the important concepts of LCM and HCF problems, definitions, formulas, and methods of calculation, along with LCM HCF questions with examples.

What is the LCM and HCF Full Form?

The full form of HCF is Highest Common Factor. HCF is also called GCF, and GCF’s full form is Greatest Common Factor. The LCM full form is Lowest Common Multiple.

What is HCF?

The HCF full form is Highest Common Factor. HCF is also known as GCF (Greatest Common Factor) or GCD. GCD’s full form is (Greatest Common Divisor). The greatest common factor (GCF or GCD or HCF) for a subset of whole numbers is the largest positive integer that divides all the given numbers with zero remainders.

What is a “Factor” & HCF Examples

Factors of a number are numbers that divide the given number exactly with \(0,\) i.e., they are the exact divisors of the given numbers.
For example, the number \(15\) is divisible by \(1,\,3,\,5\) and \(15\).

Let us understand the concept of HCF with an example:

Consider two numbers: \(15\) and \(18\).

From the above figure, we can see that:
Factors of \(15: 1, 3, 5\) and \(15\)
Factors of \(18: 1, 2, 3, 6, 9\) and \(18\)

The common factors of both \(15\) and \(18\) are \(1\) and \(3.\) Here, \(3\) is the highest common factor of both numbers.

Hence, \(3\) is the HCF of \(15\) and \(18\).

What is LCM?

The full form of LCM is Lowest or the Least Common Multiple. The LCM of two or more numbers is the smallest positive integer that is divisible by all the given numbers.

Multiple: To get the multiples, multiply the number by \(1, 2, 3, 4, …\)

Let us understand the concept of LCM with an example:

Consider two numbers: \(8\) and \(12\).
The multiples of \(8\) are:
\(8×1=8,\)
\(8×2=16,\)
\(8×3=24,\)
\(8×4=32,\) and so on…

The multiples of \(12\) are:
\(12×1=12,\)
\(12×2=24,\)
\(12×3=36,\)
\(12×4=48,\) and so on…

\(24\) is the lowest common multiple from all the above multiples of \(8\) and \(12\). So, \(24\) is the LCM of \(8\) and \(12\).

Learn Relationship Between LCM and HCF

LCM and HCF Formula

The formula of HCF and LCM is nothing but the relationship between HCF and LCM. The formulas are given below:

Product of two numbers \(=\) HCF of two numbers \( \times \) LCM of two numbers

Suppose the two numbers are denoted by \(a\) and \(b.\) Then the HCF and LCM formula states that:

\(a \times b = {\rm{HCF}}\left( {a,b} \right) \times {\rm{LCM}}\left( {a,b} \right)\)

Using the above formula, we can calculate the HCF or LCM of any number if we know one of them and the two numbers.

HCF of two numbers \( = \frac{{{\rm{Product}}\,{\rm{of}}\,{\rm{two}}\,{\rm{numbers}}}}{{{\rm{LCM}}\,{\rm{of}}\,{\rm{two}}\,{\rm{numbers}}}}\)

LCM of two numbers \( = \frac{{{\rm{Product}}\,{\rm{of}}\,{\rm{two}}\,{\rm{numbers}}}}{{{\rm{HCF}}\,{\rm{of}}\,{\rm{two}}\,{\rm{numbers}}}}\)

HCF and LCM Tricks

Some of the important tricks to find the HCF and LCM are given below:

• The HCF of given numbers is never greater than any of the numbers.
• The LCM of given numbers is never less than any of the numbers.
• The HCF of two or more prime numbers is always \(1\).
• The LCM of two or more prime numbers is nothing but their product.
• The product of two numbers, \(a\) and \(b,\) is equal to the product of their HCF and LCM. It is also known as LCM and HCF formula, which we discussed above.
• We use the below formulas to calculate the HCF and LCM of fractions:
  (a) LCM of Fractions \( = \frac{{{\rm{LCM}}\,{\rm{of}}\,{\rm{Numerator}}}}{{{\rm{HCF}}\,{\rm{of}}\,{\rm{Denominator}}}}\)
  (b) HCF of Fractions \( = \frac{{{\rm{HCF}}\,{\rm{of}}\,{\rm{Numerator}}}}{{{\rm{LCM}}\,{\rm{of}}\,{\rm{Denominator}}}}\)

Finding HCF and LCM

There are mainly \(2\) methods to calculate HCF and LCM for a given set of numbers:
(i) Prime Factorization method
(ii) Division method

Calculating HCF Using Prime Factorisation Method

The prime factorization method is also known as the factor tree method. Let us understand how to find out HCF using this method:

• Step 1: Write each number as a product of its prime factors.
• Step 2: Now, list the common factors of both numbers.
• Step 3: The product of all common prime factors is the HCF (use the lower power of each common factor).

Let us discuss this method with an example.

Example: Find the highest common factor of \(12\) and \(14\).

First, write each number as a product of its prime factors.

\(12 = 3 \times {2^2}\)

\(14 = 7 \times {2^1}\)

As we know, the product of all common prime factors is the HCF. The common prime factor in this example is \(2\) (use the lower power of each common factor).

Hence, the HCF of \(12\) and \(14\) is \(2\).

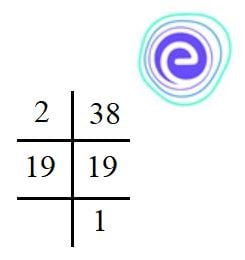
Calculating HCF Using Long Division Method

To find the HCF of any two or more numbers using the division method, let us follow the below steps:

1st Step: Write the given numbers horizontally, separated by a comma. Draw a line under the two numbers.

2nd Step: On the left side, draw a horizontal line and then write the smallest prime number that divides the given numbers without leaving any remainder. Elaborating with our example of \(8\) and \(20\):

3rd Step: Now, divide both numbers by the lowest prime number and write the quotients, separated by a comma, under the horizontal line.

4th Step: Repeat Step \(2\) and \(3\) until you reach the stage wherein no more common prime factor is available.

5th Step: The numbers on the left-hand side (inside the red box) are the common prime factors of the given numbers. To find the HCF, just multiply all the numbers present on the left (marked in red).

Hence, the HCF of \(8\) and \(20\) is \(2×2=4.\)

Calculating LCM Using Prime Factorisation

To calculate the LCM, we need to use the common prime factors for all the numbers. Take the example of finding LCM of \(8\) and \(20\). First, we need to write the prime factors of each of the given numbers.

So,

\(8=2 \times 2 \times 2\)

\(20=2 \times 2 \times 5\)

Now, we must find the maximum occurrences of each of these factors in any number.

For this example,

The factor \(2=3\) times

The factor \(5=1\) time

To find the LCM, we have to multiply each factor the highest number of times it occurs in any number. 

Hence, the LCM of \(8\) and \(20=2×2×2×5=40.\)

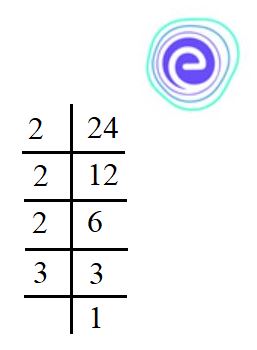
Finding LCM by Division Method

To calculate the LCM of any two or more numbers using the long division method, we will use the same technique as we used to find the HCF. The only difference will be in the final step. Instead of multiplying all the common factors present on the left-hand side, we multiply all numbers obtained at the end of the division.

Let us understand this method with an example. Suppose we must find the LCM of \(12\) and \(18\) using the long division method.

So, after performing all the division, we get:

To find the LCM, we multiply all the numbers marked in red. So, LCM of \(12\) and \(18=2×3×2×3=36\).

HCF and LCM Problems

Find the HCF and LCM of \(6, 72\) and \(120\), using the prime factorization method.

Answer:

Let us find the prime factors of all the given numbers,

\(6=2 \times 3\)

\(72=2^{3} \times 3^{2}\)

\(120=2^{3} \times 3 \times 5\)

Here, \(2^{1}\) and \(3^{1}\) are the smallest powers of the common factors \(2\) and \(3\), respectively.

So, HCF \((6,72,120)=2^{1} \times 3^{1}=2 \times 3=6\)

\({2^3},\,{3^2}\) and \(5^{1}\) are the greatest powers of the prime factors \(2, 3\) and \(5\) respectively involved in the three numbers.

So, LCM \((6,72,120)=2^{3} \times 3^{2} \times 5^{1}=360\).

HCF and LCM questions- Solved Examples

Q.1: Find out the LCM of \(48\) and \(300\).
Ans: Here, we need to find out the LCM of \(48\) and \(300\).
Prime factors of \(48=2 \times 2 \times 2 \times 2 \times 3=2^{4} \times 3^{1}\)
Prime factors of \(300=2 \times 2 \times 3 \times 5 \times 5=2^{2} \times 3^{1} \times 5^{2}\)
List all numbers found, as many times as they occur, most often any one given number, and multiply them together to find the LCM.
Thus, \(2^{4} \times 3^{1} \times 5^{2}=1200\)
Hence, the LCM of \(48\) and \(300\) is \(1200\).

Q.2: Find the LCM of \(12, 18, 30\).
Ans: Here, we need to find the LCM of \(12,18,30\).
Now, let us find the prime factors of the above three numbers.
The prime factors of \(12=2 \times 2 \times 3=2^{2} \times 3^{1}\)
The prime factors of \(18=2 \times 3 \times 3=2^{1} \times 3^{2}\)
The prime factors of \(30=2 \times 3 \times 5=2^{1} \times 3^{1} \times 5^{1}\)
Now, list all the prime numbers found as many times as they occur most often for anyone given number and multiply them together to find the LCM.
So, \(2 \times 2 \times 3 \times 3 \times 5=180\)
Using exponents instead, multiply together each of the prime numbers with the highest power
Thus, \(2^{2} \times 3^{2} \times 5^{1}=180\)
Hence, the LCM of \(12,18,30\) is \(180\).

Q.3: Two numbers are in the ratio of \(5:11\). Find the number if their HCF is \(7\).
Ans: The ratio of two numbers \(5:11\).
Let the numbers be \(5x\) and \(11x\).
Since \(5:11\) is already the reduced ratio, \(‘x’\) must be the HCF.
So, the numbers are \(5 \times 7=35\) and \(11 \times 7=77\)
Hence, the numbers are \(35\) and \(77\).

Q.4: Find the greatest number which on dividing \(70\) and \(50\) leaves remainders \(1\) and \(4\) respectively.
Ans: The required number leaves the remainder \(1\) and \(4\) on dividing \(70\) and \(50\) respectively.
This means that the number exactly divides \(69\) and \(46\).
So, we need to find the HCF of \(69\) is \((3 \times 23)\) and \(46\) is \((2 \times 23)\).
Now, the HCF of \(69,46=23\)
Hence, the required number is \(23\).

Q.5: Find the least number, which, when divided by \(5, 7, 9\) and \(12\), leaves the same remainder \(3\) in each case.
Ans: In this type of question, we need to find the LCM of the divisors and add the common remainder (i.e., \(3\)) to it.
Let us find the LCM of \(5, 7, 9, 12\).
Thus,

The LCM of \(5,7,9,12=3 \times 5 \times 7 \times 3 \times 4=1260\)
Now, the required number \(=1260+3=1263\)
Hence, the least number is \(1263\).

Summary

In this article, you have been provided with all the necessary information regarding HCF and LCM, such as the HCF full form and LCM full form, their definitions, HCF and LCM formula, the properties, the tricks to find HCF and LCM, finding HCF and LCM of two or more numbers and some related practice problems. It will help the students understand this topic and clarify their doubts about solving problems.

FAQs Related to HCF and LCM