Plane: Definition, Representation, Formulas, Examples

Plane: There are three basic concepts in geometry: point, line, and plane. A point is a location in any space that is represented by a dot (.). It lacks any length, height, shape, or size. A line is defined as a series of points connected by a straight path.

Typically, a line is defined by two points. A plane is a surface with no depth. It is a two-dimensional object that extends indefinitely. Examples of a plane are a desktop, whiteboard, sheet of paper, laptop screen, wall, and door. Let us learn to determine the equation of the plane in the three-dimensional space that can be defined with the normal vector and the given point on the plane. 

What is a Plane?

LEARN EXAM CONCEPTS ON EMBIBE

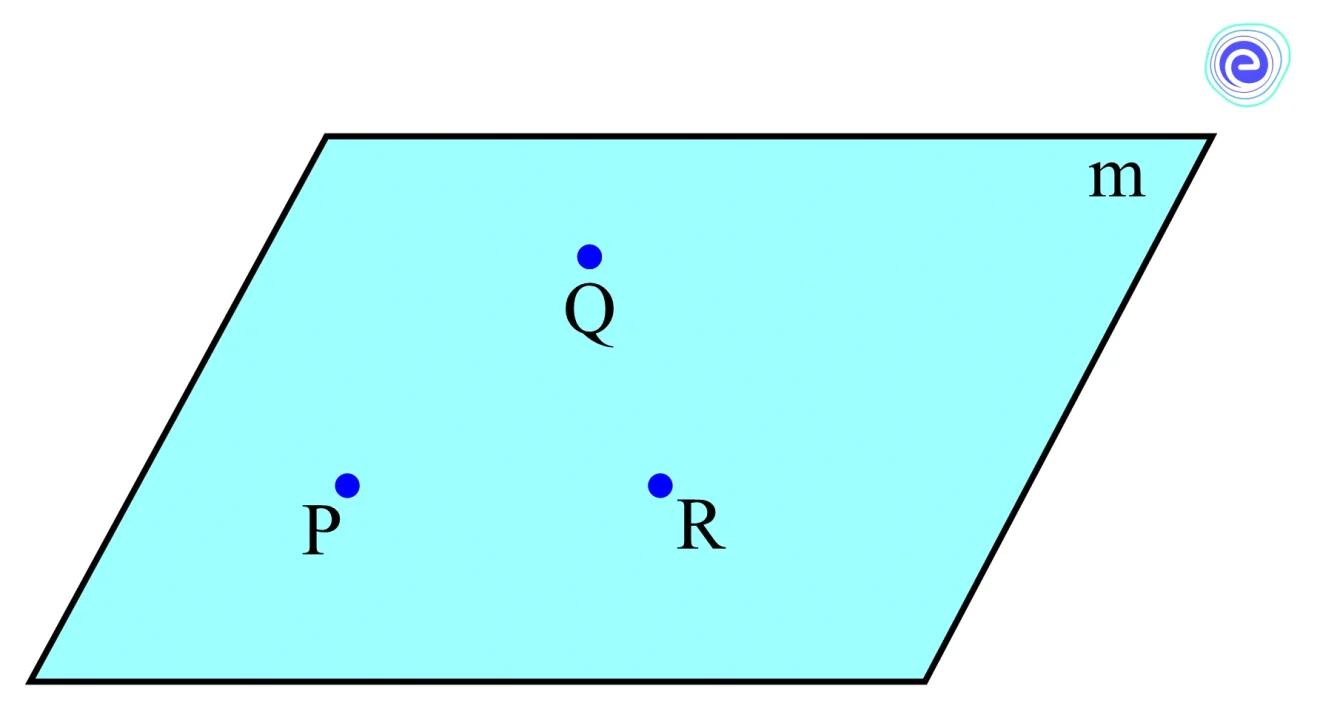
In geometry, a plane is a surface that contains all of the straight lines that connect any two points on it. In other words, it is a level or flat surface.

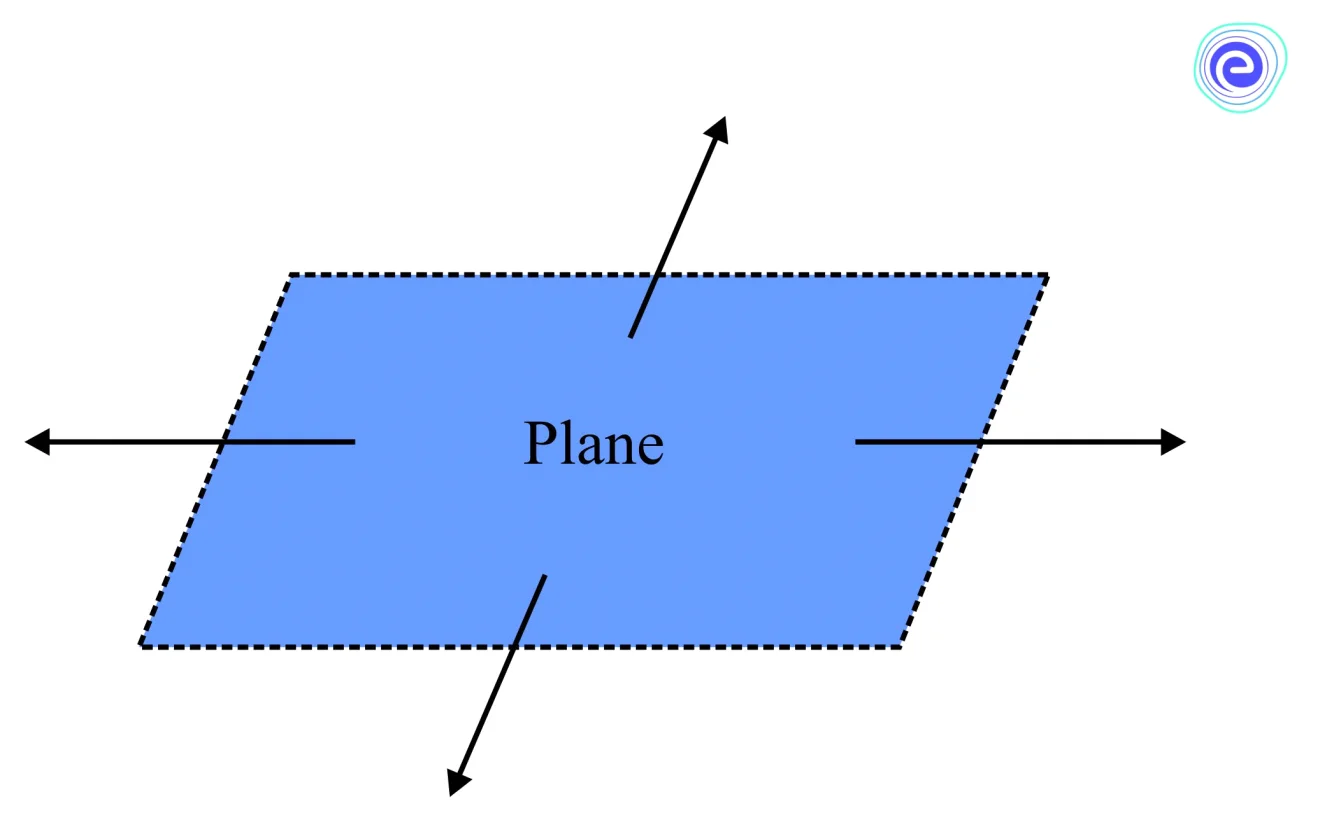
Arrows represent that it extends indefinitely along the \(x-\) and \(y-\) axes. However, it is critical to understand that the plane has no edges. It extends indefinitely in all directions. The plane has two measurements: length and width. Estimating its dimensions is impossible since the plane is infinitely large.

We can draw a four-sided figure to represent a plane, as shown below.

A plane is defined uniquely in a Euclidean space of any number of dimensions by any of the following:

• Three non-collinear points

• Using a point and a line

• Using two intersecting lines

• Using two parallel lines

Identifying a Plane in a Three-Dimensional Space

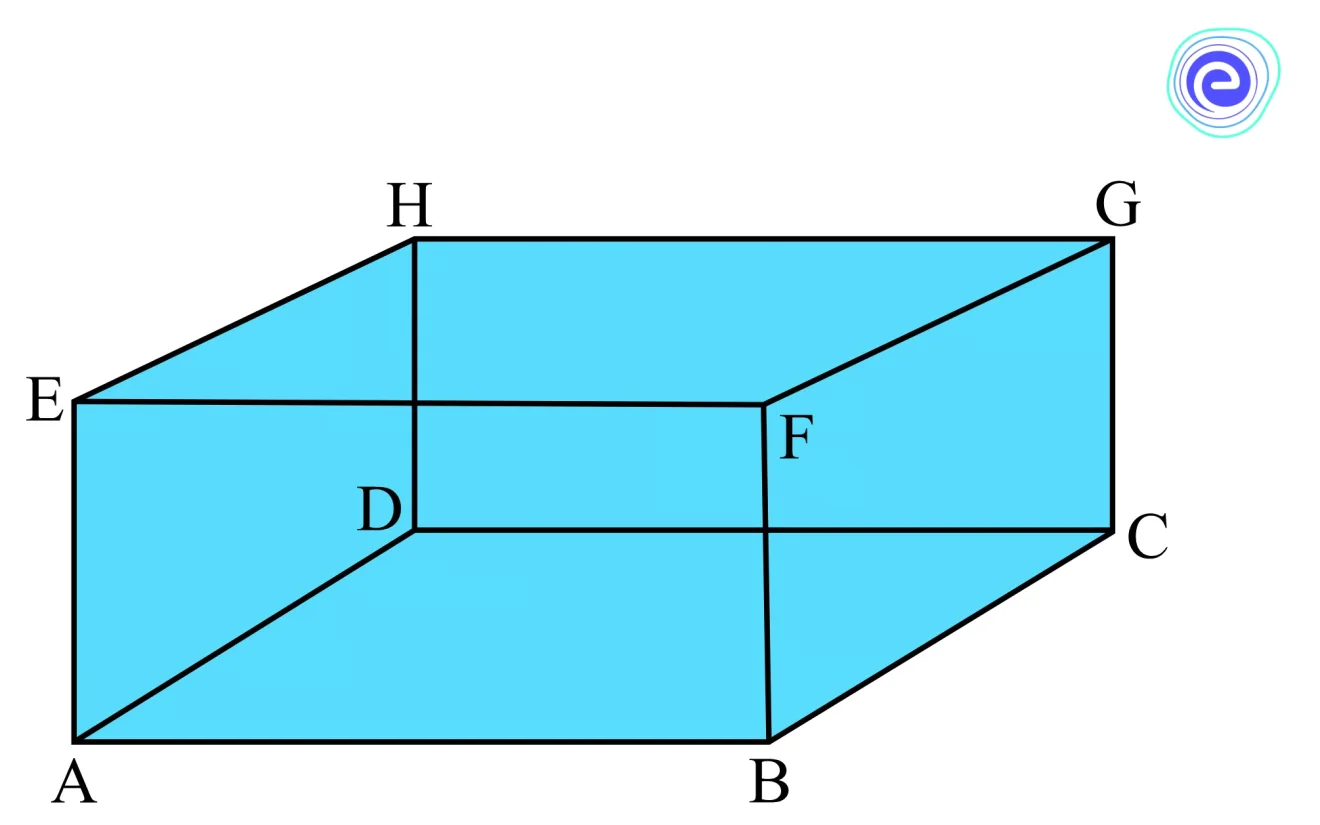
Planes are all the flat surfaces on any one side of a three-dimensional space. For example, in the cuboid shown below, all six faces are planes: \(A E F B, B F G C, C G H D, D H E A, E H G F\), and \(ADCB\)

Types of Plane Relations

In three-dimensional space, two planes can be one of the following

• Parallel
• Identical
• Intersecting

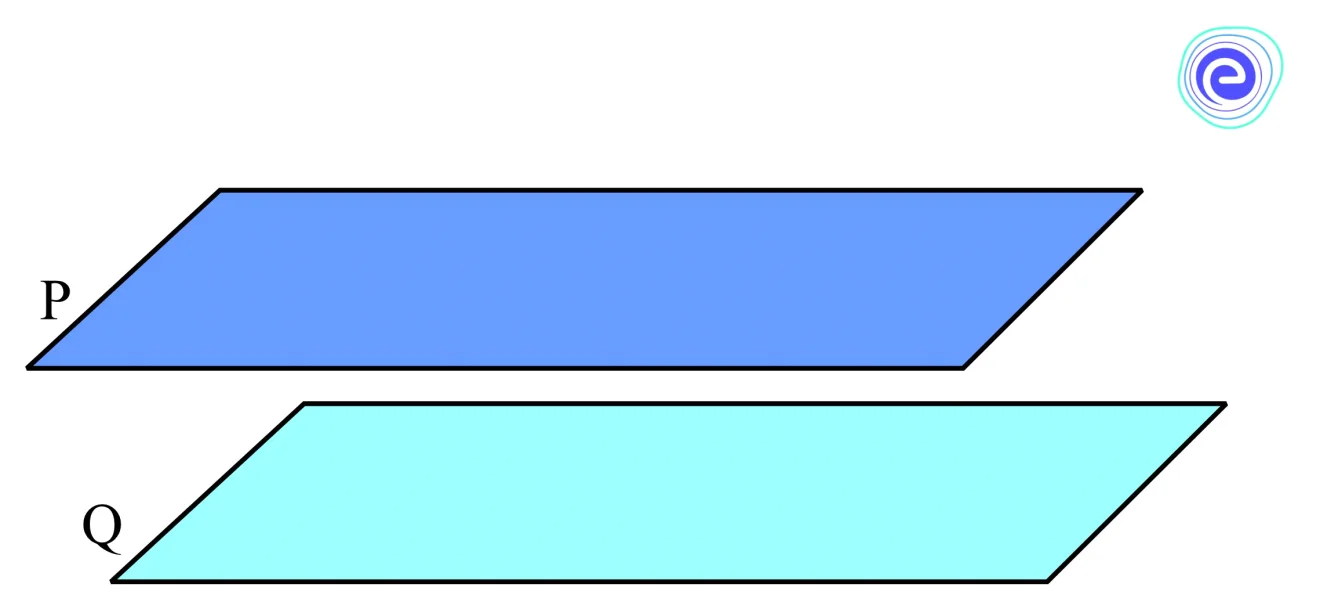
Parallel Planes

We know that two parallel objects do not intersect each other. The figure below depicts two planes, \(P\) and \(Q\), that do not intersect. Hence, they are parallel planes.

Examples:

• Opposite walls in a four-walled room
• Ceiling and floor

Plane Figures

A plane figure is a geometric figure with no thickness. It is contained in one plane. A plane figure can be formed using line segments, curves, or a combination of the two.

Example:

Circles, rectangles, triangles, and squares.

These are depicted in the figure below:

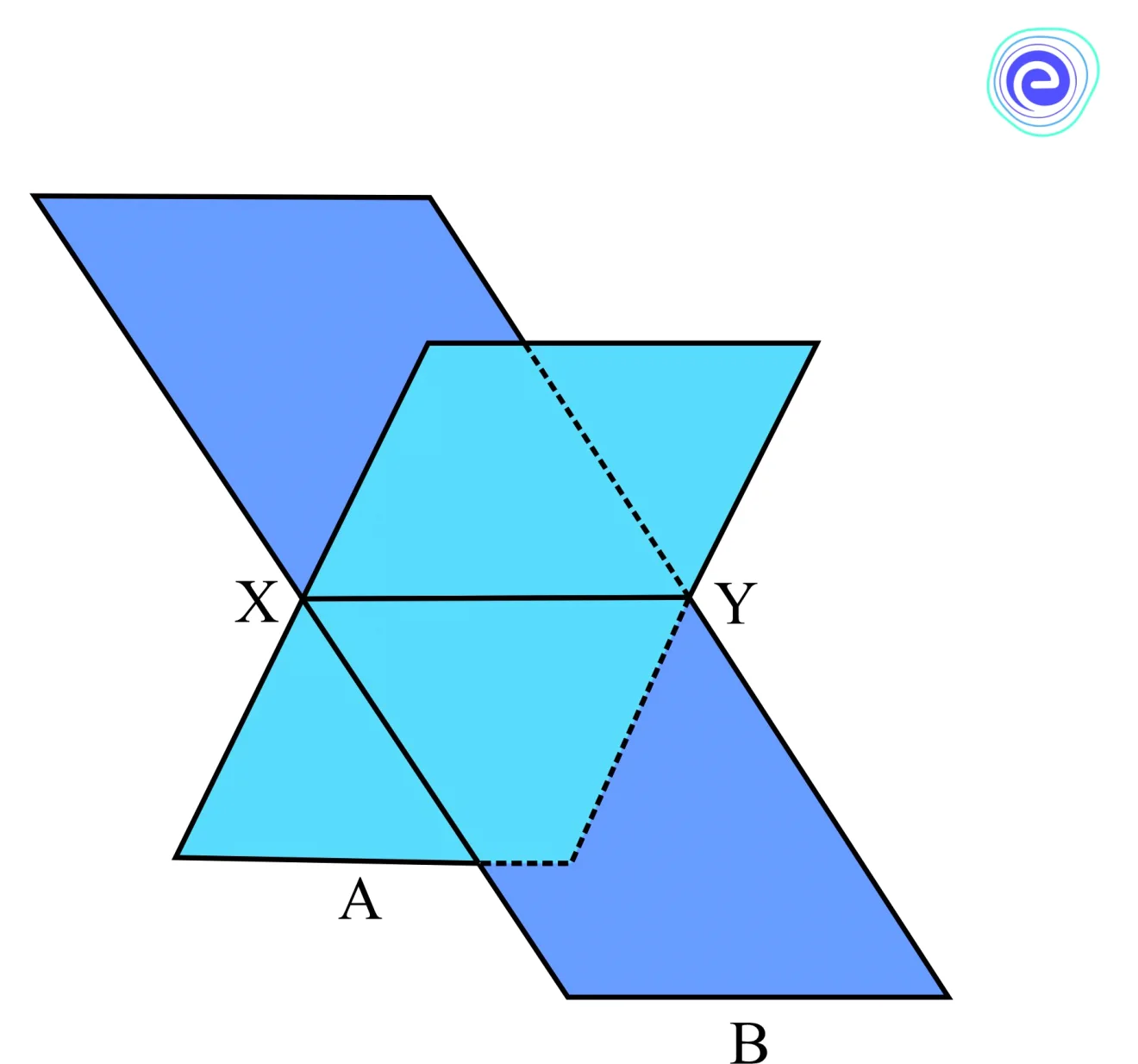
Intersecting Planes

Non-parallel planes that intersect along a line are called intersecting planes. Two planes cannot intersect more than once. The two planes, \(A\) and \(B\), are shown intersecting in a single line \(XY\) in the figure below.

Hence, \(XY\) is the common line connecting the planes \(A\) and \(B\). The two connecting walls are an example of intersecting planes in real life.

The figure below depicts two intersecting planes.

PRACTICE EXAM QUESTIONS AT EMBIBE

Properties of a Plane

• In three-dimensional space, if there are two different planes, they are either parallel or intersecting in a line.
• A line and a plane can be parallel, intersect at a point, or exist in the plane itself.
• If a pair of lines are perpendicular to a plane, they must be parallel lines.
• If two distinct planes are perpendicular to a line, they are parallel planes.

Equation of a Plane

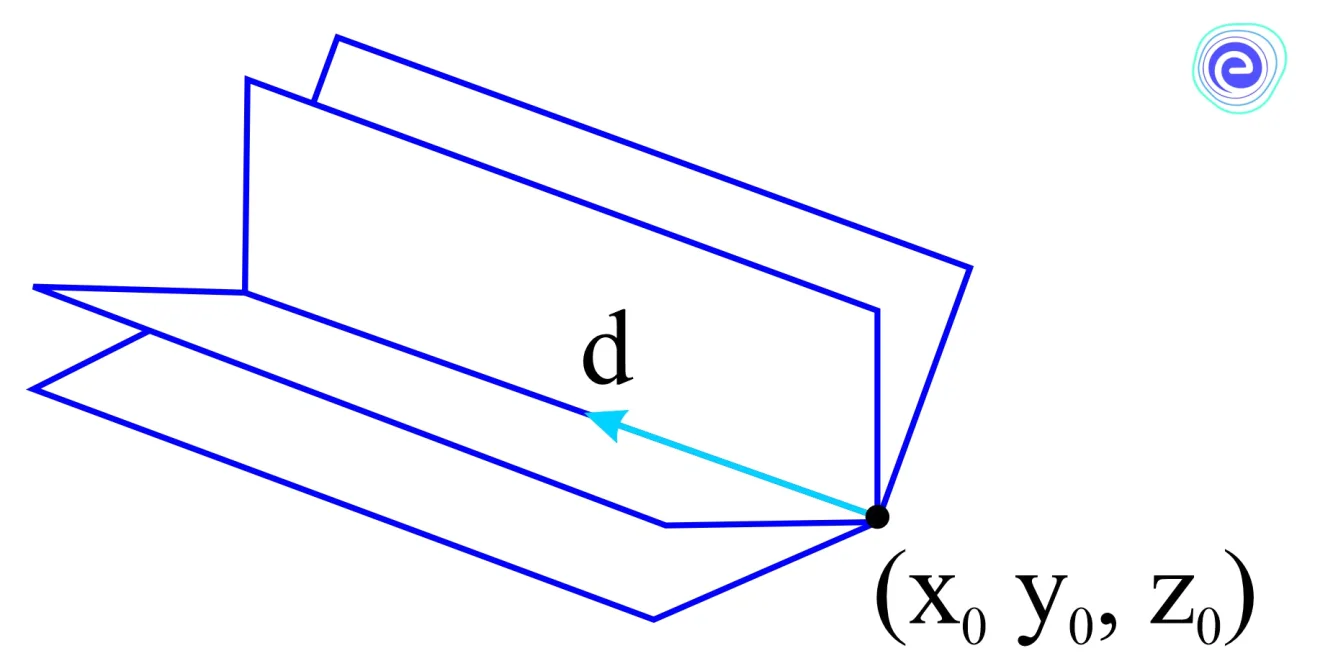
Specifying a point \(\left(x_{0}, y_{0}, z_{0}\right)\) on a plane, and a vector \(d\) parallel to the plane does not uniquely determine the plane because it is to rotate about \(d\).

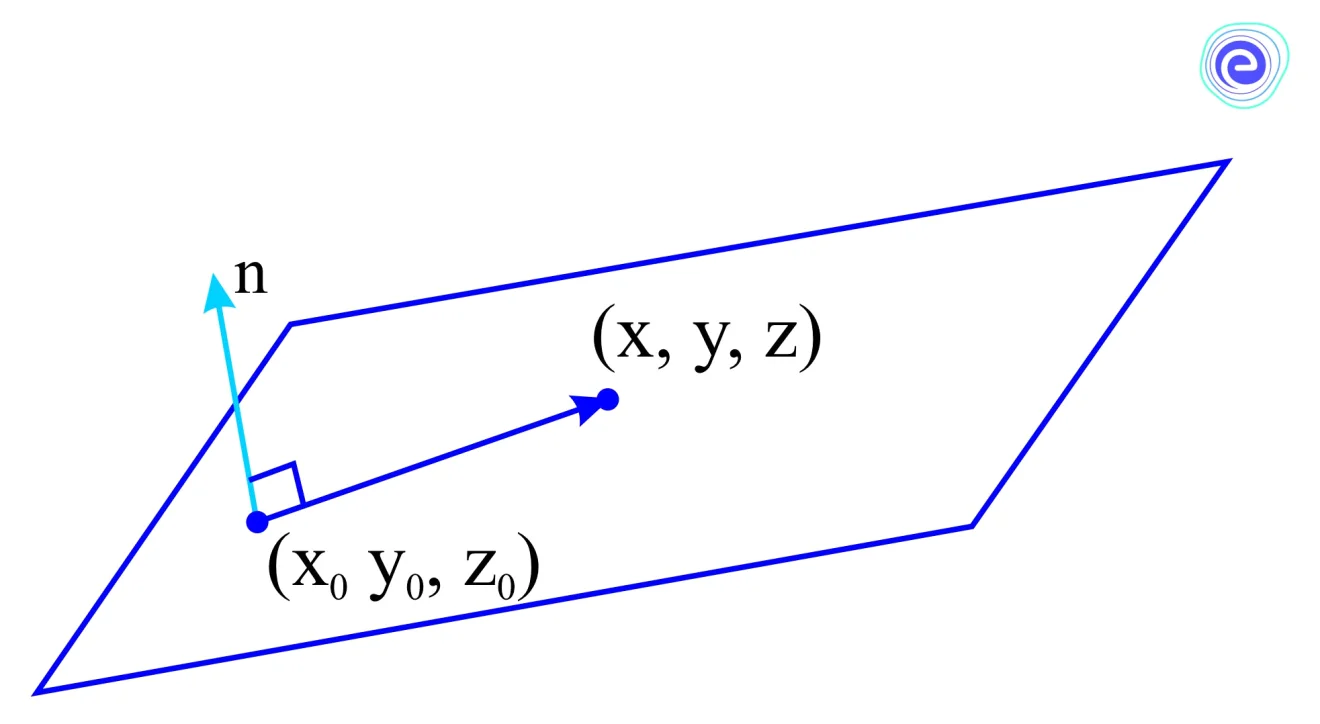
Whereas having one point that lies on the plane and one vector \(n=\left\langle n_{x}, n_{y}, n_{z}\right\rangle\) with the direction perpendicular to the plane does uniquely determine the plane.

If \((x, y, z)\) is a point on the plane, then the vector \(\left\langle x-x_{0}, y-y_{0}, z-z_{0}\right\rangle\), whose tail is at \(\left(x_{0}, y_{0}, z_{0}\right)\) and whose head is at \((x, y, z)\), lies entirely inside the plane and must be perpendicular to \(n\).
A plane can be determined uniquely if any one of the following is known:

1. A normal and its distance from the origin
2. A passing-through point and a perpendicular vector
3. Three passing through non-collinear points

Plane with Normal and Distance from Origin (Normal Form)

Vector Form

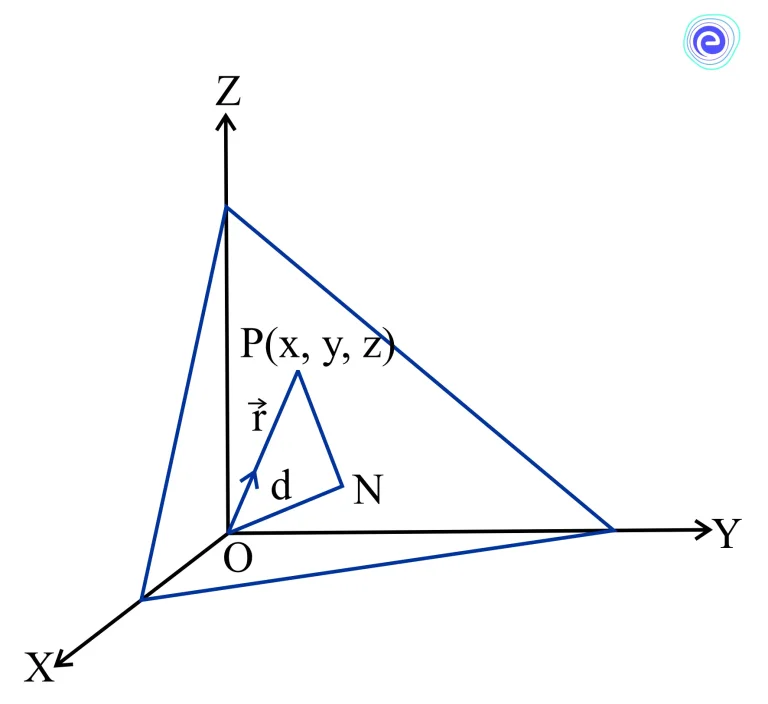
Consider a plane whose perpendicular distance from the origin is \(d,d \neq 0\). If \(\overrightarrow{O N}\) is the normal from the origin to the plane, and \(\hat{n}\) is the unit normal vector along \(\overrightarrow{O N}\). Then

\(\overrightarrow{O N}=d \hat{n}\)

Let \(P(x, y, z)\) be any point on the plane. Therefore, \(\overrightarrow{N P}\) is perpendicular to \(\overrightarrow{O N}\).

Therefore, \(\overrightarrow{N P} \cdot \overrightarrow{O N}=0\)
Let \(\hat{r}\) be the position vector of the point \(P\), then \(\overrightarrow{N P}=\hat{r}-d \hat{n}\)
\(\Rightarrow \overrightarrow{N P} \cdot \overrightarrow{O N}=(\hat{r}-d \hat{n}) \cdot d \hat{n}=0\)
\(\Rightarrow(\hat{r}-d \hat{n}) \cdot \hat{n}=0\)
\(\Rightarrow \hat{r} \cdot \hat{n}-d \hat{n} \cdot \hat{n}=0\)
Since \(\hat{n} \cdot \hat{n}=1\)
\(\hat{\boldsymbol{r}} \cdot \widehat{\boldsymbol{n}}=\boldsymbol{d}\)
This is the vector equation of the plane.

Cartesian Form

In Cartesian form, this can be written as

\((x \hat{\imath}+y \hat{\jmath}+z \hat{k}) \cdot(l \hat{\imath}+m \hat{\jmath}+n \hat{k})=d\)

\(\Rightarrow l x+m y+n z=d\)

If \(\vec{r} \cdot(a \hat{\imath}+b \hat{\jmath}+c \hat{k})=d\) is the vector equation of a plane, then \(a x+b y+c z=d\) is the Cartesian equation of the plane, where \(a,b\) and \(c\) are the direction ratios of the normal to the plane.

Plane Perpendicular to Vector and Passing Through Point

Vector Form

In the space, there can be many planes that are perpendicular to the given vector, but when given with a passing-through point \(P\left(x_{1}, y_{1}, z_{1}\right)\), only one such plane exists.

Let a plane pass through a point \(A\) with a position vector \(\vec{a}\) and perpendicular to the vector \(\vec{N}\). Let \(\vec{r}\) be the position vector of any point \(P(x, y, z)\) in the plane. Then, \(P\) lies in the plane if and only if \(\overrightarrow{A P}\) is perpendicular to \(\vec{N}\).

\(\therefore \overrightarrow{A P} \cdot \vec{N}=0\)

\(\Rightarrow(\vec{r}-\vec{a}) \cdot \vec{N}=0\)

This is the vector equation of the plane.

Cartesian Form

In Cartesian form, we can represent this as

\(\left(\left(x-x_{1}\right) \hat{\imath}+\left(y-y_{1}\right) \hat{\jmath}+\left(z-z_{1}\right) \hat{k}\right) \cdot(A \hat{\imath}+B \hat{\jmath}+C \hat{k})=0\)

\(\therefore A\left(x-x_{1}\right)+B\left(y-y_{1}\right)+C\left(z-z_{1}\right)=0\)

Plane Passing Through Three Non-Collinear Points

Vector Form

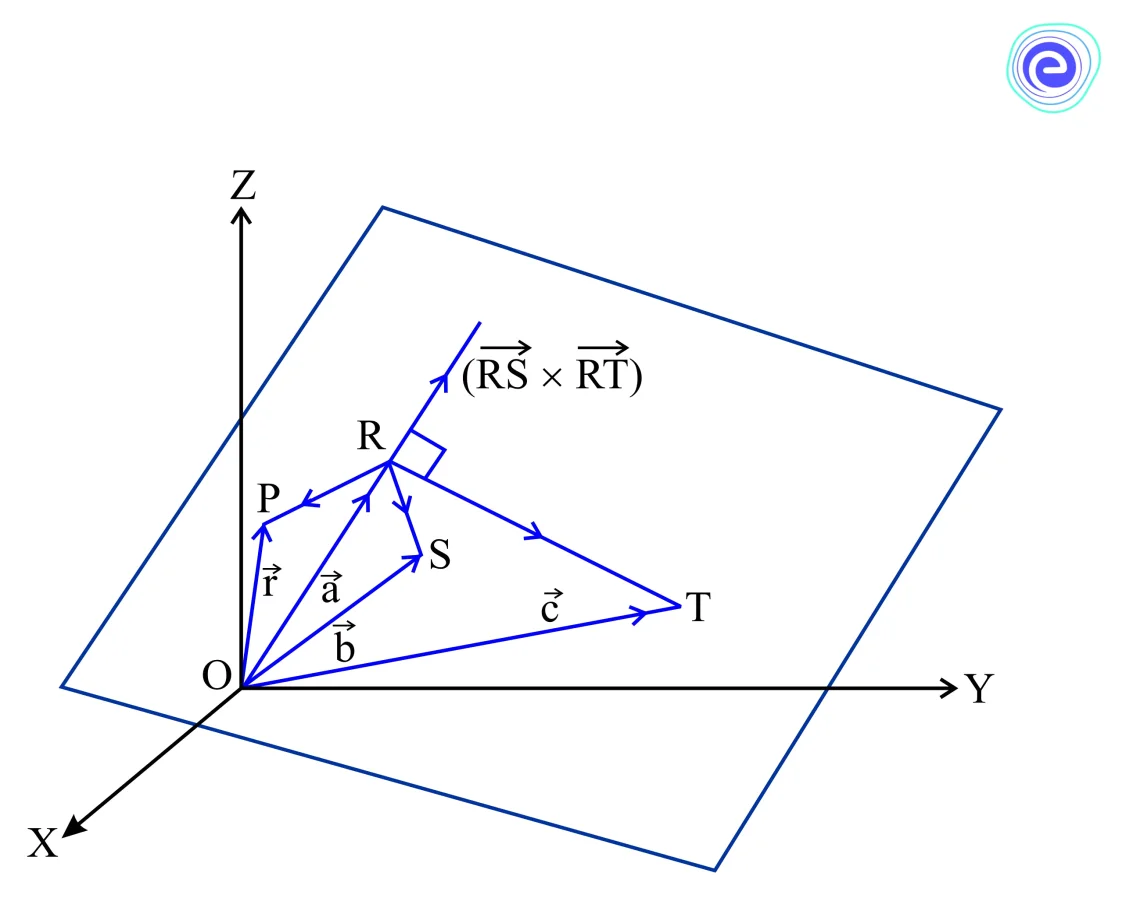
Let \(R,S\) and \(T\) be three non-collinear points on a plane with position vectors \(\vec{a}, \vec{b}\) and \(\vec{c}\), respectively.

The vectors \(\overrightarrow{R S}\) and \(\overrightarrow{R T}\) lie in the given plane. Therefore, the vector \(\overrightarrow{R S} \times \overrightarrow{R T}\) is perpendicular to the plane containing points \(R,S\) and \(T\). Let \(\vec{r}\) be the position vector of any point \(P\) in the plane.
Hence, the equation of a plane passing through \(R\) and perpendicular to the vector \(\overrightarrow{R S} \times\) \(\overrightarrow{R T}\) is

\((\vec{r}-\vec{a}) \cdot(\overrightarrow{R S} \times \overrightarrow{R T})=0\)

\((\overrightarrow{\boldsymbol{r}}-\overrightarrow{\boldsymbol{a}}) \cdot[(\overrightarrow{\boldsymbol{b}}-\overrightarrow{\boldsymbol{a}}) \times(\overrightarrow{\boldsymbol{c}}-\overrightarrow{\boldsymbol{a}})]=\mathbf{0}\).

This is the vector equation of the plane in vector form passing through three non-collinear points.

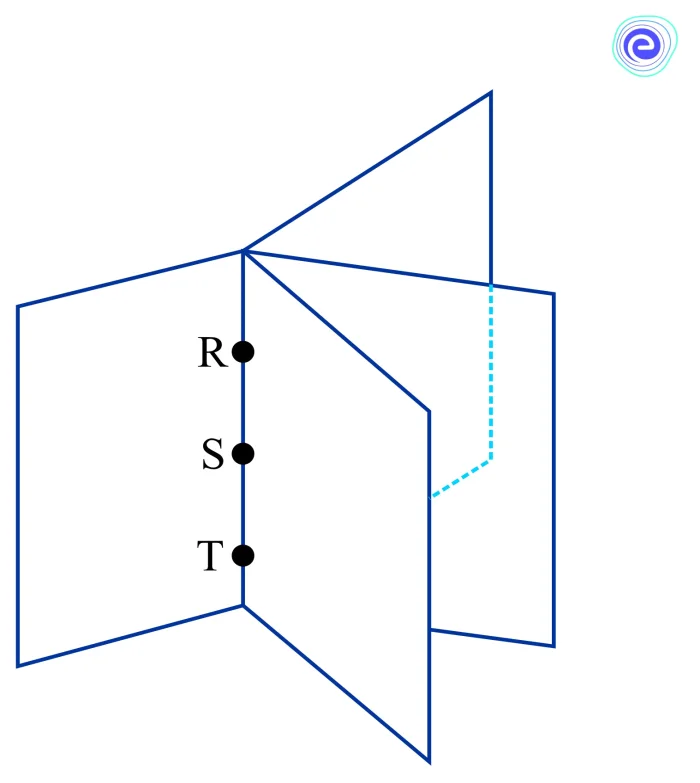
If three points were on the same line, there would be many planes containing them. These planes will resemble the pages of a book where the line containing the points \(R,S\) and \(T\) are in the binding of the book.

Cartesian Form

Let \(\left(x_{1}, y_{1}, z_{1}\right),\left(x_{2}, y_{2}, z_{2}\right)\) and \(\left(x_{3}, y_{3}, z_{3}\right)\) be the coordinates of the points \(R,S\) and \(T\), respectively. Let \((x, y, z)\) be the coordinates of any point \(P\) on the plane with the position vector \(\vec{r}\).
Then

\(\overrightarrow{R P}=\left(\left(x-x_{1}\right) \hat{\imath}+\left(y-y_{1}\right) \hat{\jmath}+\left(z-z_{1}\right) \hat{k}\right)\)

\(\overrightarrow{R S}=\left(\left(x_{2}-x_{1}\right) \hat{\imath}+\left(y_{2}-y_{1}\right) \hat{\jmath}+\left(z_{2}-z_{1}\right) \hat{k}\right)\)

\(\overrightarrow{R T}=\left(\left(x_{3}-x_{1}\right) \hat{\imath}+\left(y_{3}-y_{1}\right) \hat{\jmath}+\left(z_{3}-z_{1}\right) \hat{k}\right)\)

Substituting these values in the equation,

\((\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]=0\)

Expressing it in the form of a determinant, we have

\(\left| {\begin{array}{*{20}{c}}{\left( {x – {x_1}} \right)}&{\left( {y – {y_1}} \right)}&{\left( {z – {z_1}} \right)}\\{\left( {{x_2} – {x_1}} \right)}&{\left( {{y_2} – {y_1}} \right)}&{\left( {{z_2} – {z_1}} \right)}\\{\left( {{x_3} – {x_1}} \right)}&{\left( {{y_3} – {y_1}} \right)}&{\left( {{z_3} – {z_1}} \right)}\end{array}} \right| = 0\)

This is the equation of the plane in Cartesian form passing through three non-collinear points \(\left(x_{1}, y_{1}, z_{1}\right),\left(x_{2}, y_{2}, z_{2}\right)\) and \(\left(x_{3}, y_{3}, z_{3}\right)\).

Equation of a Plane in Intercept Form

The equation of the plane is \(A x+B y+C z+D=0\)

Let the plane make intercepts \(a,b,c\) on \(x,y\) and \(z\) axes, respectively. Hence, the plane meets \(x,y\) and \(z\)-axes at \((a, 0,0),(0, b, 0),(0,0, c)\), respectively.

Then we have

\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)

This is the required equation of the plane in the intercept form.

Solved Examples on Plane

We have provided some solved example on Plane below:

Q.1. Determine the vector equation of a plane that is at a distance of \(\frac{6}{\sqrt{29}}\) from the origin. The normal vector from the origin is \(2 \hat{i}-3 \hat{\jmath}+4 \hat{k}\).
Sol: Let \(\vec{n}=2 \hat{\imath}-3 \hat{\jmath}+4 \hat{k}\)
Then
\(\hat{n}=\frac{\vec{n}}{|\vec{n}|}\)
\(=\frac{2 \hat{\imath}-3 \hat{\jmath}+4 \hat{k}}{\sqrt{4+9+16}}\)
\(=\frac{2 \hat{\imath}-3 \hat{\jmath}+4 \hat{k}}{\sqrt{29}}\)
\(\therefore\) The vector equation of the plane is
\(\vec{r} \cdot\left(\frac{2}{\sqrt{29}} \hat{\imath}+\frac{-3}{\sqrt{29}} \hat{\jmath}+\frac{4}{\sqrt{29}} \hat{k}\right)=\frac{6}{\sqrt{29}}\)

Q.2. Find the vector equations of the plane passing through the points \(\mathbf{R}(2,5,-3), S(-2,-3,5)\) and \(T(5,3,-3)\)
Sol: Let \(\vec{a}=2 \hat{\imath}+5 \hat{\jmath}-3 \hat{k}\)
\(\vec{b}=-2 \hat{\imath}-3 \hat{\jmath}+5 \hat{k}\)
\(\vec{c}=5 \hat{\imath}+3 \hat{\jmath}-3 \hat{k}\)
Then, the vector equation of a plane passing through \(\vec{a}, \vec{b}\) and \(\vec{c}\) and is given by
\((\vec{r}-\vec{a}) \cdot(\overrightarrow{\mathrm{RS}} \times \overrightarrow{\mathrm{RT}})=0\)
\((\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]=0\)
\(\Rightarrow[\vec{r}-(2 \hat{\imath}+5 \hat{\jmath}-3 \hat{k})] \cdot[(-4 \hat{\imath}-8 \hat{\jmath}+8 \hat{k}) \times(3 \hat{\imath}-2 \hat{\jmath})]=0\)

Q.3. Find the vector equation and cartesian equation of the plane that passes through the point \((5,2,-4)\) and is perpendicular to the line whose direction ratios are \(2,3,-1\).
Sol: The position vector of \((5,2,-4)\) is \(\vec{a}=5 \hat{\imath}+2 \hat{\jmath}-4 \hat{k}\)
Normal vector \(\vec{N}\) perpendicular to the plane as \(\vec{N}=2 \hat{\imath}+3 \hat{\jmath}-\hat{k}\)
The vector equation of a plane, \((\vec{r} \rightarrow \vec{a}) \cdot \vec{N}=0\)
\([\vec{r}-(5 \hat{\imath}+2 \hat{\jmath}-4 \hat{k})] \cdot(2 \hat{\imath}+3 \hat{\jmath}-\hat{k})=0\)
Transforming into Cartesian form, we have
\([(x-5) \hat{\imath}+(y-2) \hat{\jmath}+(z+4) \hat{k}] \cdot(2 \hat{\imath}+3 \hat{\jmath}-\hat{k})=0\)
\(\Rightarrow 2(x-5)+3(y-2)-1(z+4)=0\)
\(\Rightarrow 2 x+3 y-z=20\) is the required Cartesian equation of the plane.

Q.4. Calculate the direction cosines of the unit vector perpendicular to the plane \(\vec{r} \cdot(6 \hat{\imath}-3 \hat{\jmath}-2 \hat{k})+1=0\) passing through the origin.
Sol: The given equation can be written as
\(\vec{r} \cdot(-6 \hat{\imath}+3 \hat{\jmath}+2 \hat{k})=1\) ——-(1)
Now,
\(|-6 \hat{\imath}+3 \hat{\jmath}+2 \hat{k}|=\sqrt{36+9+4}\)
\(=7\)
Therefore, by dividing both sides of \((1)\) by \(7\) , we get
\(\vec{r} \cdot\left(-\frac{6}{7} \hat{\imath}+\frac{3}{7} \hat{\jmath}+\frac{2}{7} \hat{k}\right)=\frac{1}{7}\)
which is the equation of the plane in the form \(\vec{r} \cdot \hat{n}=d\).
Here, \(\hat{n}=-\frac{6}{7} \hat{\imath}+\frac{3}{7} \hat{\jmath}+\frac{2}{7} \hat{k}\) is a unit vector perpendicular to the plane through the origin.
Hence, the direction cosines of \(\hat{n}\) are \(\frac{-6}{7}, \frac{3}{7}, \frac{2}{7}\).

Q.5. Find the equation of a plane whose intercepts are \(2,3\) and \(4\) on the \(x,y\) and \(z-\) axis, respectively.
Sol: The required equation of the plane in the intercept form
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
Here \(a=2, b=3, c=4\).
Substituting the values of \(a,b\) and \(c\) in \((1)\), we get the required equation of the plane
\(\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1\)
\(\Rightarrow 6 x+4 y+3 z=12\)

Summary

A plane is a two-dimensional surface that extends indefinitely. A plane has a thickness of zero, a curvature of zero, an infinite width, and an infinite length. It is difficult to imagine a plane in real life; all of the flat surfaces of a cube or cuboid and the flat surface of paper are real examples of geometric planes.

Planes can appear as infinitely expanded sub-spaces of some multidimensional space, such as one of the room’s walls, or they can exist independently, as in the setting of Euclidean geometry.

Parallel planes and intersecting planes are the two types of planes. Parallel planes are two non-intersecting planes, and planes that intersect at \({90^0}\) are called perpendicular planes.

FAQs on Plane

The frequently asked questions on Plane are given below:

Q.1. What is a plane?
Ans: In Mathematics, a plane is a flat, two-dimensional surface that extends infinitely. A plane has no thickness, no curvature, infinite width, and infinite length.

Q.2. Why is a plane two-dimensional?
Ans: A plane has zero thickness, zero curvature, infinite width, and infinite length. The plane only has two dimensions, length and width, so it is a two-dimensional object.

Q.3. What is the equation of a plane in intercept form?
Ans: The equation of the plane in the intercept form is given by
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
Here, \(a,b,c\) are the intercepts of the plane on \(x,y\) and \(z\) axes, respectively.

Q.4. What is the equation of a plane in normal form?
Ans: The equation of the plane in vector form is given by
\(\hat{r} \cdot \hat{n}=d\)
In Cartesian form, we can write this as
\((x \hat{\imath}+y \hat{\jmath}+z \hat{k}) \cdot(l \hat{\imath}+m \hat{\jmath}+n \hat{k})=d\)
\(\Rightarrow lx+m y+n z=d\)

Q.5. What is the equation of a plane passing through three non-colinear points in Cartesian form?
Ans: If expressed in the form of a determinant, we have
\(\left| {\begin{array}{*{20}{c}}{\left( {x – {x_1}} \right)}&{\left( {y – {y_1}} \right)}&{\left( {z – {z_1}} \right)}\\{\left( {{x_2} – {x_1}} \right)}&{\left( {{y_2} – {y_1}} \right)}&{\left( {{z_2} – {z_1}} \right)}\\{\left( {{x_3} – {x_1}} \right)}&{\left( {{y_3} – {y_1}} \right)}&{\left( {{z_3} – {z_1}} \right)}\end{array}} \right| = 0\)
is the equation of the plane in Cartesian form passing through three non-collinear points \(\left(x_{1}, y_{1}, z_{1}\right),\left(x_{2}, y_{2}, z_{2}\right)\) and \(\left(x_{3}, y_{3}, z_{3}\right)\).

ATTEMPT MOCK TESTS ON EMBIBE

We hope this article on Plane is helpful to you. If you have any queries related to this page, ping us through the comment box below and we will get back to you as soon as possible.