Second Order Derivative: Representation, Examples

Second Order Derivative: The concept of second-order derivatives, if simply put, is the derivative of the first-order derivative of the given function. The first-order derivative at a point gives us the slope of the tangent at that point or the instantaneous rate of change of that function at that point. Similarly, the second-order derivatives are used to get an idea of the shape of the graph of a given function.

They classify the behaviour of a function in terms of concavity. A second-order derivative is the derivative of the first-order derivative of a function. So, we have to find the derivative of a function and then draw out the derivative of the first derivative. A first-order derivative can be written as \(f^{\prime}(x)\) or \(\frac{d y}{d x}\) and the second-order derivative as \(f^{\prime \prime}(x)\) or \(\frac{d^{2} y}{d x^{2}}\).

Learn 10th CBSE Exam Concepts

Second Order Derivatives

A derivative is a rate at which one quantity, say \(y\), changes with another quantity, say \(x\). Differentiation is the process of determining a function’s derivative. A first-order derivative provides you with the slope of a function at any point.

If \(f(x)\) is a function differentiable in the interval \([a,b]\), at every point of the interval, the derivative of the function exists finitely, and it is unique. There exists a new function \(g(x)=\) \(f^{\prime}(x)\) and this \(f^{\prime}(x)\) is the first derivative of the function \(f(x)\), which is denoted by \(\frac{d}{d x} f(x)\) or \(\frac{d f(x)}{d x}\) or \(D f(x)\) or \(f^{\prime}(x)\).

The derivative of the first-order derivative of a function is known as the second-order derivative. The second derivative, or the second-order derivative, of a function \(f\) is the derivative of the first derivative of \(f\).

The second-order derivative offers us an understanding of the shape of a function’s graph.

The second derivative of the function \(f(x)\) is commonly denoted as \(f^{\prime \prime}(x)\).

If \(y=f\), it is sometimes expressed as \(D^{2} y\) or \(\frac{d^{2} y}{d x^{2}}\) or \(y^{\prime \prime}(x)\).

Consider \(y=f(x)\)

Then, the first-order derivative is \(\frac{d y}{d x}=f^{\prime}(x)\)

If \(f^{\prime}(x)\) is differentiable, we can differentiate it with respect to \(x\) once more. The left-hand side thus becomes \(\frac{d}{d x}\left(\frac{d y}{d x}\right)\), often known as the second-order derivative of \(y\) with respect to \(x\).

Significance of Second-Order Derivative

The second-order derivative calculates the rate of change of a quantity as it changes. For example, the second-order derivative of the position of the object with respect to time is the instantaneous acceleration of that object. In simpler words, the rate at which the velocity of the object changes with respect to time.

On the graph of a function, the second-order derivative corresponds to the curvature or concavity of the graph. A second-order derivative is used to determine the points of inflection. 

The graph of a function with a positive second-order derivative is upwardly concave, while that with a negative second-order derivative curve is in the opposite direction.

Second-Order Derivative Test

The first derivative graphically represents the slope of a function at any point, while the second derivative represents the slope changes with respect to the independent variable in the graph. The curvature of the given graph is explained by the second derivative of a function with a variable slope. The second derivative defines the nature of the given function. The second derivative test determines the maxima, minima, and points of inflection of a function.

When we calculate the first derivative, we will get the critical points and equate that to \(0\). Then we have to find the second-order derivative and substitute the critical values. The value thus obtained determines whether the critical point is maxima or minima or a point of inflection.

If \(f^{\prime \prime}(x)<0\), then the function \(f(x)\) has a local maximum at \(x\).

If \(f^{\prime \prime}(x)>0\), then the function \(f(x)\) has a local minimum at \(x\).

If \(f^{\prime \prime}(x)=0\), then it is not possible to conclude anything about the point \(x\), a possible point of inflection.

The second-order derivative of a given function corresponds to the curvature or concavity of the graph.

• If the value of the second-order derivative is positive, the graph of a function is upwardly concave.
• If the value of the second-order derivative is negative, the graph of a function is downwardly open.

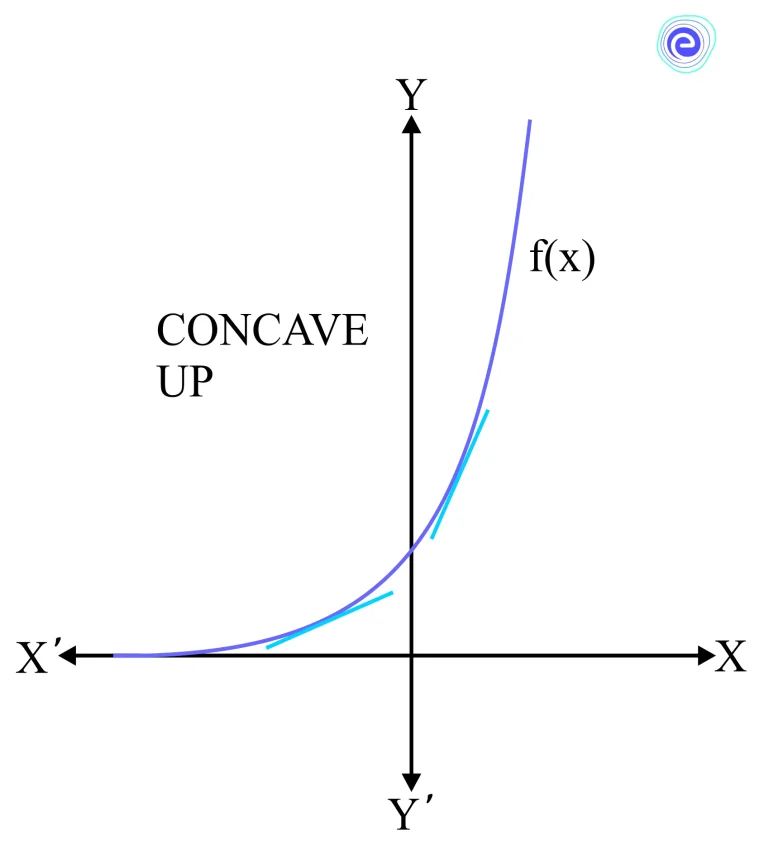
Concave Up

The second-order derivative of a function is said to be concave up or simply concave at the point \((c, f(c))\), if \(\frac{d^{2} f}{d x^{2}}=c>0\). In such cases, the neighbouring points of the function \(c\) will lie above the line on the graph that will be the tangent at \((c, f(c))\).

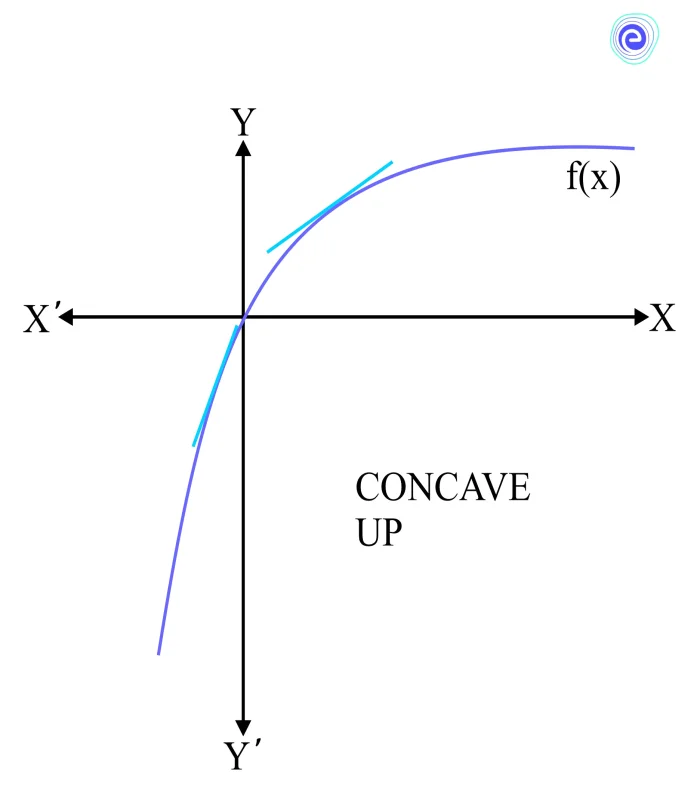
Concave Down

Concave down, or convex, is said to be a function if its second-order derivative, \(\frac{d^{2} f(c)}{d x^{2}}=c<\) 0 at a point \((c, f(c))\). In such cases, the neighbouring points of the function \(c\) will lie below the straight line tangent to the graph at the point \((c, f(c))\).

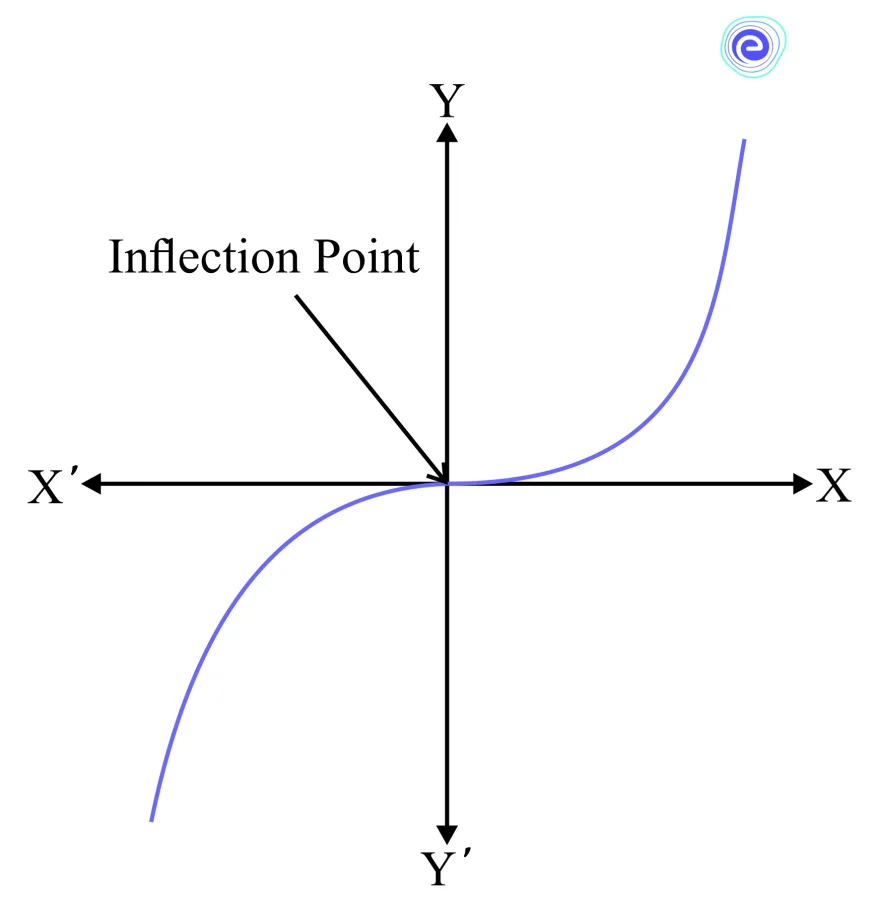
Point of Inflection

The point of inflection is a point on the function’s graph where the curve changes from concave down to concave up or concave up to concave down. At this point, the sign of the second-order derivative is accordingly changed from positive to negative or from negative to positive.

At this point, the function’s second-order derivative is zero.

Practice 10th CBSE Exam Questions

Solved Examples of Second Order Derivative

Below are a few solved examples that can help in getting a better idea.

Q.1. A function is defined as \(y=x^{3}\). Find \(\frac{d^{2} y}{d x^{2}}\).
Sol:
Given: \(y=x^{3}\)
The first derivative of the function will be \(\frac{d y}{d x}=\frac{d}{d x}\left(x^{3}\right)\)
\(=3 x^{2}\)
We have to differentiate further to find its second-order derivative.
\(\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}\left(\frac{d y}{d x}\right)\)
\(=\frac{d}{d x}\left(3 x^{2}\right)\)
\(=6x\)
Hence, the second-order derivative of the given function is \(6x\).

Q.2. \(f(x)\) is a trigonometric function defined as \(f(x)=\sin 3x\). Find its second-order derivative.
Sol: Given: \(f(x)=\sin 3x\)
The second-order derivative of a function \(f\) is the derivative of the first derivative of \(f\).
So, the first-order derivative of the function is
\(\frac{d y}{d x}=\frac{d}{d x}(\sin 3 x)\)
\(=3 \cos 3 x\)
We have to differentiate further to find its second-order derivative.
\(\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}\left(\frac{d y}{d x}\right)\)
\(=\frac{d}{d x}(3 \cos 3x)\)
\(=-9 \sin 3x\)
Hence, the second-order derivative of the given function is \(-9 \sin 3x\).

Q.3. Find the second-order derivative of the polynomial function \(y = 3{x^4} – 2{x^3} + 4{x^2} – 5x + 1\)
Sol: Given: \(y=3 x^{4}-2 x^{3}+4 x^{2}-5 x+1\)
The second-order derivative, of a function \(f\) is the derivative of the derivative of \(f\).
So, the first order derivative of the function is
\(\frac{d y}{d x}=\frac{d}{d x}\left(3 x^{4}-2 x^{3}+4 x^{2}-5 x+1\right)=12 x^{3}-6 x^{2}+8 x-5\)
We have to differentiate further to find its second-order derivative.
\(\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}\left(\frac{d y}{d x}\right)\)
\(=\frac{d}{d x}\left(12 x^{3}-6 x^{2}+8 x-5\right)\)
\(=36 x^{2}-12 x+8\)
Hence, the second-order derivative of the given function is \(36 x^{2}-12 x+8\)

Q.4. Find \(y^{\prime \prime}\) if \(y\) is defined as \(y=e^{x}\).
Sol: Given: \(y=e^{x}\)
The second-order derivative of a function \(f\) is the derivative of the derivative of \(f\).
So, the first-order derivative of the function is
\(\frac{d y}{d x}=\frac{d}{d x}\left(e^{x}\right)\)
\(=e^{x}\)
We have to differentiate further to find its second-order derivative.
\(\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}\left(\frac{d y}{d x}\right)\)
\(=\frac{d}{d x}\left(e^{x}\right)\)
\(=e^{x}\)

Q.5. Find the second-order derivative of the function \(y=e^{-x^{2}}\).
Sol: Given function is \(y=x\)
The second-order derivative of a function \(f\) is the derivative of the first derivative of \(f\).
So, the first-order derivative of the function is
\(\frac{d y}{d x}=\frac{d}{d x}(x)\)
\(=1\)
We have to differentiate further to find its second-order derivative.
\(\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}\left(\frac{d y}{d x}\right)\)
\(=\frac{d}{d x}(1)\)
\(=0\)
Hence, the second-order derivative of \(y=x\) is \(0\) .

Summary

A derivative provides the slope of a function at any point in time. The second-order derivative is the derivative of a function’s first derivative. The first-order derivative at that point determines the slope of the tangent at that point or the instantaneous rate of change of a function at that point. The second-order derivative offers us an understanding of the shape of a function’s graph.

The second derivative of the function \(f(x)\) is commonly abbreviated as \(f^{\prime \prime}(x)\). If \(y=f\), it is sometimes expressed as \(D^{2} y\) or \(\frac{d y^{2}}{d x^{2}}\), or \(y^{\prime \prime}(x)\). The second derivative test helps check whether the given point is maxima, minima or point of inflection. It also helps to classify the behaviour of a function in terms of concavity.

FAQs on Second Order Derivative

Students might be having many questions regarding the Second Order Derivative. Here are a few commonly asked questions and answers.

Q.3. What is the representation for the second derivative?
Ans: The first derivative of the function \(f(x)\), that is denoted by \(\frac{d}{d x} f(x)\) or \(\frac{d f(x)}{d x}\), or \(Df(x)\), or \(f^{\prime}(x)\). The second derivative of the function \(f(x)\) is commonly abbreviated as \(f^{\prime \prime}(x)\). If \(y=f\), it is sometimes expressed as \(D^{2}y\) or \(\frac{d^{2} y}{d x^{2}}\), or \(y^{\prime \prime}(x)\).

Q.4. What does the second derivative test tell you about the graph of a function?
Ans: On the graph of a function, the second-order derivative corresponds to the curvature or concavity of the graph. A second-order derivative is used to determine the points of inflection. 
The graph of a function with a positive second-order derivative is upwardly concave, while the graph of a function with a negative second-order derivative curves in the opposite direction.

Q.5. How can we find whether a point is local minima?
Ans: We have to find the second-order derivative and substitute the critical values. The value thus obtained determines whether the critical point is maxima or minima or a point of inflection.

• If \(f^{\prime \prime}(x)<0\), then the function \(f(x)\) has a local maximum at \(x\).
• If \(f^{\prime \prime}(x)>0\), then the function \(f(x)\) has a local minimum at \(x\).
• If \(f^{\prime \prime}(x)=0\), then it is not possible to conclude anything about the point \(x\), a possible point of inflection.

Attempt 10th CBSE Exam Mock Tests

We hope this information about the Second Order Derivative has been helpful. If you have any doubts, comment in the section below, and we will get back to you.