Two General Theorems on Indefinite Integrals: Proofs

Two General Theorems on Indefinite Integrals: In calculus, finding an antiderivative is a crucial step. It is used to calculate the area under a curve as well as a variety of physical and electrical equations that scientists and engineers utilise daily. Leibniz proposed the idea of integration. It is the method of finding \(a(x)\) whose derivative \(\frac{d}{d x} a(x)\) is equal to \(b(x)\).

This is antiderivation, also known as indefinite integration, reverses the differentiation process. The two theorems on indefinite integrals are also known as fundamental theorems of calculus. They are also called general theorems. The first theorem gives the relation between differentiation and integration. The second theorem evaluates the definite integrals and is also called the evaluation theorem.

Two General Theorems on Indefinite Integrals: Definition

Indefinite integration is simply known as integration. “Integral is based on a limiting approach that approximates the area of a curved region by splitting the region into thin vertical slabs,” says mathematician Bernhard Riemann.

\(\int f(x) d x\) represents standard forms of integration of the function \(f(x)\). The area under the curve of \(f(x)\) is determined by the integration \(f(x)\). The complete class of antiderivatives is sometimes known as integration, and it is written as the indefinite integral of \(f\) with regard to \(x\).

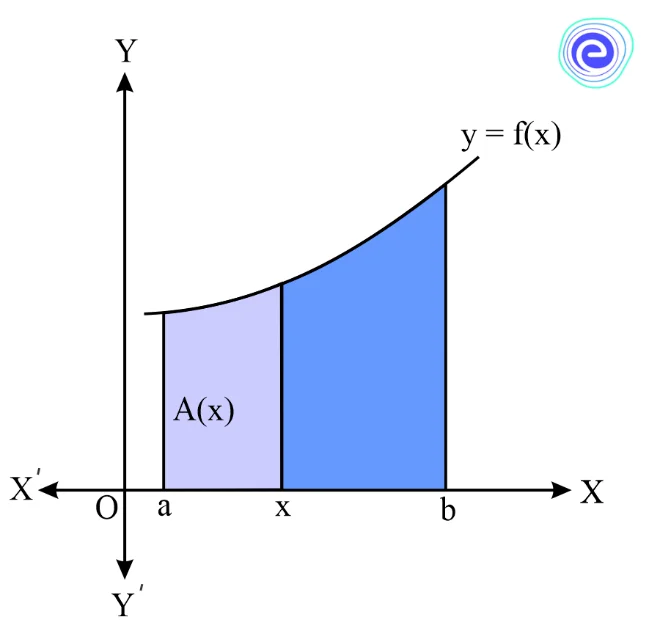
Integration as an Area Function

Let us consider a function \(y=f(x)\), which is continuous over the interval \([a, b]\), then the area bounded by the curves and \(x\)-axis is given by

\(\int_{a}^{b} f(x) d x\)

Let \(x\) be any point in the interval \([a, b]\).

Then, \(\int_{a}^{x} f(x) d x\) is the area of the curve between the limits \(a\) and \(x\). This function is represented by \(A(x)\), and it is known as the area function.

\(A(x)=\int_{a}^{b} f(x) d x\)

Where, \(x \in[a, b]\) and \(f(x)>0\)

Indefinite Integral Theorems

The two general theorems on indefinite integrals are powerful theorems in Mathematics, and these establish the link between differentiation and integration. These two allow us to evaluate definite internals without having to calculate areas or use Riemann sums.

The two general theorems on indefinite integrals are

1. First fundamental theorem of calculus
   \(\frac{d}{d x} \int_{a}^{b} f(t) d t=f(x)\)
2. Second fundamental theorem of calculus
   \(\int_{a}^{b} f(x) d x=F(b)-F(a)\)

Theorem 1: First Theorem on Indefinite Integral

The first theorem on indefinite integral is used to calculate the derivative of an integral as it establishes the relationship between the derivative and the integral.

We can evaluate the derivative of a definite integral without evaluating the definite integral using this theorem.

Statement

If a function \(f(x)\) is continuous over the closed interval \([a, b]\) and differentiable over the open interval \((a, b)\), and \(F(x)\) is defined as \(F(x)=\int_{a}^{x} f(t) d t\), then \(F^{\prime}(x)=f(x)\) over the closed interval \([a, b]\).

Mathematical Statement

\(\frac{d}{d x} \int_{a}^{x} f(t) d t=f(x)\)

Proof

It is given that, \(\int_{a}^{x} f(t) d t=F(x) \cdots(i)\)

From the definition of the derivative of a function,

\({F^\prime }(x) = \mathop {\lim }\limits_{h \to 0} \frac{{F(x + h) – F(x)}}{h} \cdots (ii)\)

From \((i)\) and \((ii)\)

\({F^\prime }(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{1}{h}} \right)\left( {\int_a^{x + h} f (t)dt – \int_a^x f (t)dt} \right) \cdots (iii)\)

This equation represents the area under the curve \(y=f(t)\) over the interval \([x, x+h]\).

Then, according to the definition of area function,

\({F^\prime }(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{1}{h}} \right)\int_a^{x + h} f (t)dt\)

Now, form the mean value theorem, if there exists a limit \(c\), such that \(x \leq c \leq x+h\), then

\(f(c)=\frac{1}{h} \int_{a}^{x+h} f(t) dt\)

Thus, \({F^\prime }(x) = \mathop {\lim }\limits_{h \to 0} f(c) \cdots (iv)\)

Since \(c\) lies in the interval \([x, x+h]\)

So, \(h \rightarrow 0, c \longrightarrow x\)

Thus, \(\mathop {\lim }\limits_{h \to 0} f(c) = \mathop {\lim }\limits_{c \to x} f(c) = f(x) \cdots (v)\)

Now, from \((iv)\) and \((v)\),

\(F^{\prime}(x)=f(x)\)

Hence, proved \(f(x)\) is continuous function.

Theorem 2: Second Theorem on Indefinite Integral

The second theorem on indefinite integrals is used to evaluate the definite integrals. So, it is also called an evaluation theorem. It is an extremely useful theorem. It allows us to calculate the definite integral without finding the sum’s limit. Finding a function whose derivative equals the integrand is the most important step in assessing a definite integral. The link between differentiation and integration is strengthened as a result.

The value of the antiderivative \(F\) of function \(f\) at the upper limit \(b-\) the same antiderivative value at the lower limit \(a\), gives the value of \(\int_{a}^{b} f(x) d x\), where \(f(x)\) is a well-defined and continuous function over the interval \([a, b]\).

Statement

If a function \(f(x)\) is well-defined and continuous over the interval \([a, b]\) and \(F(x)\) be the antiderivative of the function \(f(x)\), then \(\int_{a}^{b} f(x) d x=\) (value of the antiderivative \(F\) of \(f\) at the upper limit \(b-\) value of the same antiderivative at the lower limit \(a\)).

Mathematical Statement

\(\int_{a}^{b} f(x) d x=F(b)-F(a)\)

where \(F(x)\) is the ant-derivative of \(f(x)\)

Proof

Let us consider a function \(y=x_{i}\), where \(i=1,2, \ldots n\) and it is having regular partition over the interval \([a, b]\).

So, \(F(b)-F(a)=\left[F\left(x_{n}\right)-F\left(x_{0}\right)\right]\)

\(F(b)-F(a)=\sum_{i=1}^{n}\left[F\left(x_{i}\right)-F\left(x_{i-1}\right)\right]-(i)\)

Given theta, \(F\) is the antiderivative of \(f\) over the interval \([a, b]\)

According to the mean value theorem \(c_{i}\) belongs to \(\left[x_{i-1}, x_{i}\right]\) and \(i=1,2,3,4, \ldots n\)

\(\left[F\left(x_{i}\right)-F\left(x_{i-1}\right)\right]=\mathrm{F}^{\prime}\left(c_{i}\right)\left(x_{i}-x_{i-1}\right)\)

We know that, \(F^{\prime}\left(c_{i}\right)=f\left(c_{i}\right)\) and \(\left(x_{i}-x_{i-1}\right)=\Delta x\)

\(\left[F\left(x_{i}\right)-F\left(x_{i-1}\right)\right]=f\left(c_{i}\right) \Delta x-(ii)\)

From \((i)\) and \((ii)\),

\(F(b)-F(a)=\sum_{i=1}^{n} f\left(c_{i}\right) \Delta x\)

\(\mathop {\lim }\limits_{n \to \infty } [F(b) – F(a)] = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n f \left( {{c_i}} \right)\Delta x \cdots (iii)\)

From the first theorem on indefinite integral,

\(\mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n f \left( {{c_i}} \right)\Delta x = \int_a^b f (x)dx \cdots (iv)\)

From \((iii)\) and \((iv)\),

\(F(b)-F(a)=\int_{a}^{b} f(x) d x\)

Hence, proved.

Solved Examples

Q.1. Find the value of \(\frac{d}{d x} \int_{3}^{x} \frac{2+t}{3+t^{3}} dt\) by using the first theorem of indefinite integral.

Ans: Given: \(\frac{d}{d x} \int_{3}^{x} \frac{2+t}{3+t^{3}} dt\)

Comparing \(\frac{d}{d x} \int_{3}^{x} \frac{2+t}{3+t^{3}} dt\) with \(\frac{d}{d x} \int_{a}^{x} f(t) dt\), we get

\(f(t)=\frac{2+t}{3+t^{3}}\)

The first theorem of indefinite integral tells that if the function \(f(x)\) is continuous over the closed interval \([a, b]\) and differentiable over the open interval \((a, b)\), and \(F(x)\) is defined as

\(F(x)=\int_{a}^{x} f(t) d t\), then \(\frac{d}{d x} \int_{a}^{x} f(t) d t=f(x)\)

\(\Rightarrow \frac{d}{d x} \int_{3}^{x} \frac{2+t}{3+t^{3}} d t=f(x)\)

\(\therefore \frac{d}{d x} \int_{3}^{x} \frac{2+t}{3+t^{3}} d t=\frac{2+x}{3+x^{3}}\)

Q.2. By using the theorem of indefinite integral, calculate the value of \(\int_{-1}^{3}\left(x^{2}-3\right) d x\)

Ans: Given: \(\int_{-1}^{3}\left(x^{2}-3\right) d x\)

First, we need to evaluate \(\int\left(x^{2}-3\right) dx\)

\(\int\left(x^{2}-3\right) d x=\int x^{2} d x-\int 3 d x\)

\(\int\left(x^{2}-3\right) d x=\frac{x^{2+1}}{2+1}-3 \int d x\)

\(\int\left(x^{2}-3\right) d x=\frac{x^{3}}{3}-3 x\)

By using the theorem on indefinite integral, \(\int_{a}^{b} f(x) d x=[F(x)]_{a}^{b}\), where \(F(x)\) is the antiderivative of \(f(x)\).

• \(\int_{1}^{3}\left(x^{2}-3\right) d x=\left[\frac{x^{3}}{3}-3 x\right]_{-1}^{3}\)

\(\Rightarrow \int_{-1}^{3}\left(x^{2}-3\right) d x=\left[\frac{x^{3}}{3}\right]{-1}^{3}-[3 x]{-1}^{3}\)

\(\Rightarrow \int_{-1}^{3}\left(x^{2}-3\right) d x=\left[\frac{3^{3}}{3}-\frac{(-1)^{3}}{3}\right]-[3(3)-3(-1)]\)

\(\Rightarrow \int_{-1}^{3}\left(x^{2}-3\right) d x=\left[\frac{27}{3}+\frac{1}{3}\right]-[9+3]\)

\(\Rightarrow \int_{-1}^{3}\left(x^{2}-3\right) d x=9+\frac{1}{3}-12\)

\(\Rightarrow \int_{-1}^{3}\left(x^{2}-3\right) d x=\frac{1}{3}-3\)

\(\Rightarrow \int_{-1}^{3}\left(x^{2}-3\right) d x=\frac{1-9}{3}\)

\(\therefore \int_{-1}^{3}\left(x^{2}-3\right) d x=-\frac{8}{3}\)

Q.3. What is the value of \(\int_{0}^{1} x e^{x} d x\) ?

Ans: Given: \(\int_{0}^{1} x e^{x} d x\)

Evaluating the \(\int x \mathrm{e}^{x} d x\)

Let \(u=x\) and \(d v=e^{x} d x\).

Then, the value of \(d u=d x\) and \(v=\int d v=\int x e^{x} d x=e^{x}\)

Then, the given integration can be written as

\(\int u d v=u v-\int v d u\)

\(\Rightarrow \int x \mathrm{e}^{x} d x=x \cdot e^{x}-\int e^{x} d x\)

\(\Rightarrow x \cdot e^{x}-e^{x}+C\)

\(\Rightarrow \int_{0}^{1} x e^{x} d x=\left[x \cdot e^{x}-e^{x}\right]{0}^{1}\)

\(\Rightarrow \int{0}^{1} x e^{x} d x=\left[x e^{x}\right]{0}^{1}-\left[e^{x}\right]{0}^{1}\)

\(\Rightarrow \int_{0}^{1} x e^{x} d x=\left[1 \cdot e^{1}-0 \cdot e^{0}\right]-\left[e^{1}-e^{0}\right]\)

\(\Rightarrow \int_{0}^{1} x e^{x} d x=e-0-e+1\)

\(\therefore \int_{0}^{1} x e^{x} d x=1\)

Q.4. Find the value of \(\frac{d}{d x} \int_{0}^{\frac{\pi}{2}}(\cos t-\sin t)dt\) by using the first theorem of indefinite integral.

Ans: Given: \(\frac{d}{d x} \int_{0}^{\frac{\pi}{2}}(\cos t-\sin t) d t\)

Comparing \(\frac{d}{d x} \int_{0}^{\frac{\pi}{2}}(\cos t-\sin t) d t\) with \(\frac{d}{d x} \int_{a}^{x} f(t) d t\)

\(f(t)=\cos t-\sin t\)

The first theorem of indefinite integral tells that if the function \(f(x)\) is continuous over the closed interval \([a, b]\) and differentiable over the open interval \((a, b)\), and \(F(x)\) is defined as \(F(x)=\int_{a}^{x} f(t) d t\), then

\(\frac{d}{d x} \int_{a}^{x} f(t) d t=f(x)\)

\(\Rightarrow \frac{d}{d x} \int_{0}^{\frac{\pi}{2}}(\cos t-\sin t) d t=f(x)\)

\(\therefore \frac{d}{d x} \int_{0}^{\frac{\pi}{2}}(\cos t-\sin t) d t=\cos x-\sin x\)

Q.5. Calculate the derivative of the function \(F(x)\) , where \(F(x)=\int_{1}^{x} \sqrt{t^{2}+3 t} dt\) at \(x=3\)

Ans: Given: \(F(x)=\int_{1}^{x} \sqrt{t^{2}+3 t} dt\)

According to the first theorem of indefinite integral, \(F^{\prime}(x)=f(x)\), where \(F(x)=\int_{a}^{x} f(t) d t\)

So, \(F^{\prime}(x)=\sqrt{x^{2}+3 x}\)

The value of \(F^{\prime}(x)\) at \(x=3\) is

\(\sqrt{3^{2}+3(3)}=\sqrt{9+9}\)

\(=\sqrt{18}\)

Hence, the antiderivative of the function \(F(x)\) at \(x=3\) is \(\sqrt{18}\).

Summary

The general theorems on indefinite integrals explain how differentiation and integration are related. Gottfried Wilhelm Leibniz and Sir Isaac Newton discovered this connection in the late \(1600s\). There are two theorems associated with the indefinite integrals. The area of the region in the graph of functions is defined and calculated using integration.

The differentiation and integration are inverse processes supported by the first theorem on indefinite integral. The second theorem on indefinite integral justifies evaluating a definite integral by first evaluating the indefinite integral and then substituting the upper and lower bounds. The second theorem on indefinite integral is known as the evaluation theorem.

Frequently Asked Questions (FAQs)

The frequently asked questions on two general theorems on indefinite integrals are given below:

Q.1. What is a general indefinite integral?
Ans: An indefinite integral has no endpoints and just asks us to determine the integrand’s general antiderivative. Because it is a family of functions that differ by constants, the answer must include a ‘+ constant’ term to denote all antiderivatives.
Example: \(\int x d x=\frac{x^{2}}{2}+C\), where \(C\) is constant.

Q.2. What are the properties of indefinite integrals?
Ans: The properties of indefinite integrals are

• \(\int k f(x) d x=k \int f(x) d x\)
• \(\int-f(x) d x=-\int f(x) d x\)
• \(\int[f(x)+g(x)] d x=\int f(x) d x+\int g(x) d x\)
• \(\int[f(x)-g(x)] d x=\int f(x) d x-\int g(x) d x\)

Q.4. What are the two general theorems of indefinite integrals?
Ans: If a function \(f(x)\) is continuous over the interval \([a, b]\), then two theorems on indefinite integrals are:

• Theorem 1: If \(F(x)=\int_{a}^{b} f(x) d x\), then \(F^{\prime}(x)=f(x)\)
• Theorem 2: \(\int_{a}^{b} f(x) d x=F(b)-F(a)\), where \(F(x)\) is the antiderivative of \(f(x)\).

Q.5. How do you find the general indefinite integral?
Ans: The general indefinite integral can be found by using

• Properties of indefinite integration
• Integration by substitution
• Integration by parts
• Integration by partial fractions
• Integration by trigonometric functions

We hope this article on two general theorems on indefinite integrals is helpful to you. If you have any queries related to this page, ping us through the comment section below and we will get back to you as soon as possible.